Уравнение равновесия жидкости.

Уравнения равновесия жидкости могут быть получены из уравнений движения в напряжениях (2.16), если положить в них . Кроме того, как было показано, в покоящейся жидкости касательные напряжения не проявляются, т.е. все производные по t равны нулю. И, наконец, нормальные напряжения заменяем давлением, что дает

;

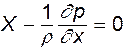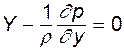; (3.1)

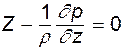
В векторной форме эта система может быть записана в форме

(3.2)

Уравнения (3.1) носят название системы дифференциальных уравнений Эйлера для гидростатики. Эта система уравнений показывает, что существует непосредственная связь между величиной гидростатического давления в точке и ее координатами. Эта связь может быть раскрыта, если проинтегрировать (3.1).

На жидкое тело могут действовать силы, имеющие различную физическую природу. Поэтому правомерна такая постановка вопроса: всегда ли под действием приложенных сил жидкость может находиться в состоянии равновесия? Для ответа на этот вопрос необходимо выполнить некоторые преобразования системы дифференциальных уравнений (3.1).