Основное уравнение гидростатики в дифференциальной форме.

Умножим каждое из уравнений, входящих в (3.1) на dx, dy и dz соответственно и просуммируем их, что даст

(3.3)

Выражение, стоящее в скобках во втором члене уравнения, есть не что иное, как полный дифференциал давления - dp, поэтому можем записать

(3.4)

Это уравнение называют основным уравнением гидростатики в дифференциальной форме. В левой части его - полный дифференциал, поэтому и правая часть также должна быть полным дифференциалом. Следовательно, силы и плотность должны быть такими функциями x, y и z, чтобы они обращали правую часть (3.4) в полный дифференциал. Если этого не происходит, то равновесие жидкости невозможно. Другими словами, если жидкость находится в состоянии равновесия, то правая часть (3.4) является полным дифференциалом какой-то функции .

Считая плотность постоянной ( 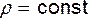), можем записать

(3.5)

Из теоретической механики известно, что скалярное произведение силы на элементарное перемещение частицы называют элементарной работой, т.е.

(3.6)

Силы, работа которых не зависит от пути движения, а только от начального и конечного положений, называют потенциальными. При этом для того, чтобы работа силы не зависела от пути движения, необходимо и достаточно, чтобы выражение для элементарной работы, т.е. (3.6), было полным дифференциалом некоторой скалярной функции P, называемой силовой. Взятая с противоположным знаком, она называется потенциалом. Таким образом, рассмотренную выше функцию можно назвать силовой функцией, а (3.4) представить как

(3.7)

Из чего следует, что несжимаемая жидкость может находиться в равновесии только под действием сил, имеющих потенциал.