
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение силы давления жидкости на поверхности тел.
Задача сводится к нахождению силы давления жидкости на поверхности стенок, ограничивающих ее.
Рассмотрим криволинейную поверхность AB произвольной формы, площадь которой S (рис. 3.3). Выделим на ней элементарную площадку dS, пусть 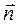 - орт внешней нормали. Сила, действующая на эту площадку
- орт внешней нормали. Сила, действующая на эту площадку


|
где p - гидростатическое давление в центре площадки. Обычно в технических приложениях интерес представляет лишь сила, возникающая от избыточного давления. Имея в виду, что  , получаем
, получаем

 (3.14)
(3.14)
На всю площадь действует сила
| Рис. 3.3 |
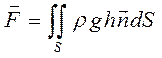 (3.15)
(3.15)
Запишем это выражение в проекциях на оси координат, что дает
 (3.16)
(3.16)
 (3.17)
(3.17)
|
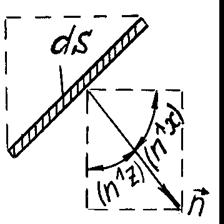
Для удобства изобразим отдельно элементарную площадку (см. рис. 3.4). Из рисунка следует, что


где  - вертикальная, и
- вертикальная, и 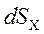 - горизонтальная проекции dS. Таким образом
- горизонтальная проекции dS. Таким образом
 (3.18)
(3.18)
| Рис. 3.4 |
 (3.19)
(3.19)
Рассмотрим горизонтальную составляющую.
Из механики известно, что интеграл (3.18) есть статический момент площади, равный произведению  , где
, где  - координата центра тяжести вертикальной проекции.
- координата центра тяжести вертикальной проекции.
Следовательно,
 (3.20)
(3.20)
т.е. горизонтальная составляющая равна произведению вертикальной проекции стенки на гидростатическое давление в центре тяжести этой проекции.
Определим теперь вертикальную составляющую силы, для чего воспользуемся следствием из формулы Гаусса-Остроградского (см. ф-лу 1.16)

Из уравнения равновесия (3.2) имеем  , т.е.
, т.е.

Вертикальная проекция единичной массовой силы  (знак плюс, т.к. в данном случае ось z ориентирована вниз).
(знак плюс, т.к. в данном случае ось z ориентирована вниз).
Следовательно,
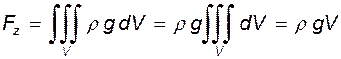 (3.21)
(3.21)

|
V носит название объема тела давления. Таким образом, вертикальная составляющая равна весу жидкости, заключенному в объеме тела давления. Для нахождения этого объема следует использовать формальное правило: тело давления - это объем, образованный криволинейной стенкой, ее проекцией на свободную поверхность (либо на продолжение свободной поверхности) и вертикальными проектирующими плоскостями. На рис. 3.5 показаны примеры определения тел давлений для двух случаев.
| Рис. 3.5 |
Как следует из рисунка, тело давления может быть как положительным, так и отрицательным (фиктивным).
Дата добавления: 2014-11-13; просмотров: 305; Мы поможем в написании вашей работы!; Нарушение авторских прав |