Уравнение движения вязкой жидкости. (уравнение Навье-Стокса)

18 марта 1822 года в докладе, представленном Французской академии наук, Клод Луи Навье писал о полученных им уравнениях: «Хотя уравнения основаны на гипотезе Ньютона о том, что касательные напряжения пропорциональны скорости деформации, никак нельзя сказать, что они не выражают ничего нового».

Уравнения движения вязкой жидкости можно получить из уравнений движения в напряжениях (2.16), выполнив некоторые преобразования. Рассмотрим лишь одну проекцию этих уравнений:

Как было показано при рассмотрении модели вязкой жидкости, нормальные напряжения

Для упрощения задачи будем считать жидкость несжимаемой ( ), тогда

(8.6)

Касательное напряжение

(8.7)

аналогично

(8.8)

Суммируя (8.6), (8.7) и (8.8) и группируя члены, получаем:

Третий член можно записать в виде:

но жидкость несжимаема, и . Таким образом получаем:

(8.9)

Выражение в скобках есть ни что иное, как оператор Лапласа - , а . Окончательно получаем:

(8.10)

Аналогично можно расписать и две другие проекции. Полученная система уравнений движения вязкой жидкости и носит название системы уравнений Навье-Стокса.

В векторной форме можно записать

(8.11)

Как следует из (8.11), это уравнение отличается от уравнения движения идеальной жидкости дополнительным членом ( ), учитывающим действие сил вязкого трения.

Целью гидродинамического расчета является нахождение полей скоростей и давлений, т.е. в результате расчета должны быть найдены четыре величины: , , 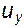и p. Принципиально это оказывается возможным, так как три уравнения Навье-Стокса (в проекциях) плюс уравнение неразрывности образуют замкнутую систему. Плотность и вязкость, входящие в них, считаются известными, а проекции массовых сил (X, Y, Z) задаются условиями конкретной задачи.

С чисто математических позиций уравнения Навье-Стокса относится к классу нелинейных дифференциальных уравнений в частных производных второго порядка. Одно из наиболее неприятных из их свойств ­ нелинейность, обусловленная наличием конвективных членов ускорения. Следует отметить, что до настоящего времени вследствие практически непреодолимых математических трудностей не получено ни одного общего решения уравнений Навье-Стокса в их полном виде, т.е. при сохранении всех конвективных членов и всех членов, учитывающих вязкость. Известны лишь отдельные частные решения.

Одним из основных граничных условий при интегрировании является условие «прилипания», т.е. равенство нулю скорости жидкости на стенке.