Расход потока и средняя скорость.

Для решения широкого круга прикладных инженерных задач плодотворной явилась введенная Эйлером так называемая струйная модель потока. Согласно этой модели поток представляется состоящим из бесконечного множества струек жидкости. При рассмотрении потока поперечные сечения в нем выбираются так, чтобы пересекающие их линии тока были нормальны к ним. В этом случае сечение потока называется «живым». Очевидно, что если линии тока параллельны, то живое сечение будет плоским.

Ранее, в разделе «Кинематика», было показано, что элемен­тарный объемный расход несжимаемой жидкости может быть определен как

(9.1)

где u -скорость в сечении струйки, dA - площадь ее поперечного сечения.

В соответствии со струйной моделью расход потока

(9.2)

Рассмотрим движение жидкости в трубе круглого поперечного сечения. В силу тормозящего действия сил вязкого трения распределение скоростей в поперечном сечении трубопровода (эпюра скорости) будет иметь вид, показанный на рис. 9.1. Для удобства перейдем к цилиндрическим координатам (r, ), где - полярный угол.

В этой системе

(9.3)

Подставляя (9.3) в (9.2) получаем

(9.4)

Имея в виду, что , имеем

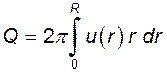(9.5)

Запись 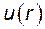обозначает, что местные скорости в сечении трубы изменяются по радиусу. Другими словами, 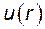описывает закон изменения скорости, т.е. является математическим описанием эпюры. Следовательно, для того, чтобы вычислить расход по (9.5), необходимо знать уравнение эпюры скорости, которое, как правило, неизвестно. Поскольку расход является важнейшим параметром, знание которого требуется при проведении любых гидравлических расчетов, необходимо найти путь, позволяющий преодолеть возникшее затруднение.

Рассмотрим, как решается эта задача в механике жидкости. С чисто математических позиций интеграл в правой части выражает объем эпюры скорости. Представим теперь, что при неизменном расходе Q в силу каких-то причин жидкость потеряла вязкость. Это, очевидно, приведет к тому, что эпюра начнет перестраиваться и, так как исчезнут силы вязкого трения, то все частицы жидкости будут двигаться с какой-то одинаковой скоростью v (см. рис. 9.1), а так как по условию расход остается тем же, то объем новой эпюры равен объему старой. При этом условии , и из (9.5) получаем

(9.6)

Скорость , введенная таким образом носит название средней либо среднерасходной скорости. Следовательно, формально средняя скорость может быть определена как фиктивная скорость, с которой должны были бы двигаться все частицы жидкости для того, чтобы расход был равен его истинному значению.

С физической точки зрения использование понятия средней скорости, одинаковой для всех частиц жидкости в сечении, позволяет свести задачу о движении жидкости в трубах и каналах к одномерной.