
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение Бернулли для потока вязкой жидкости.
Как уже отмечалось, уравнение Навье-Стокса в подавляющем большинстве случаев не поддаются интегрированию. Вместе с тем, практическая деятельность, связанная с необходимостью использования законов движения жидких сред, настоятельно требовала разработки инженерных методов расчета.
Одним из путей решения этой задачи, оказавшимся наиболее плодотворным, явился путь обобщения уравнения Бернулли, т.е. распространения его на поток вязкой жидкости. В основу этого метода, как уже отмечалось, положена струйная модель - представление о потоке как о бесконечно большой сумме струек, протекающих через сечение.
Исходим из того, что движение установившееся и в рассматриваемом сечении поток слабо деформирован. Определим энергию, проносимую секундной массой струйки через сечение (т.е. мощность струйки ). Эта величина может быть найдена как произведение полной удельной энергии струйки (  ) на ее массовый расход (
) на ее массовый расход (  ). В справедливости этого легко убедиться непосредственно. Действительно, удельная энергия -Дж/кг, массовый расход - кг/с, их произведение
). В справедливости этого легко убедиться непосредственно. Действительно, удельная энергия -Дж/кг, массовый расход - кг/с, их произведение
 .
.
Таким образом
 (9.9)
(9.9)
Секундная энергия (мощность) потока в соответствии со струйной моделью
 (9.10)
(9.10)
либо
 (9.11)
(9.11)
Так как поток слабодеформированный, то  и первый интеграл принимает вид
и первый интеграл принимает вид
 (9.12)
(9.12)
 (9.13)
(9.13)
По физическому смыслу второй член в (9.13) представляет собой кинетическую энергию секундной массы.
Поскольку мы ограничимся одномерным представлением, то в (9.13) необходимо ввести среднюю скорость. Поступим следующим образом: разделим обе части уравнения на массовый расход Q, т.е. отнесем это соотношение, как и уравнение Бернулли для струйки, к единице массы (  Дж/с;
Дж/с; 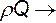 кг/с;
кг/с;  и, следовательно,
и, следовательно,  -удельная энергия.
-удельная энергия.
Таким образом, имеем
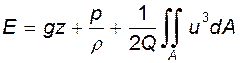 (9.14)
(9.14)
Разделив и умножив третий член на квадрат средней скорости  , с учетом того, что
, с учетом того, что 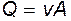 , получим
, получим
 (9.15)
(9.15)
Обозначим выражение  ; тогда
; тогда
 (9.16)
(9.16)
Величина  носит название коэффициента кинетической энергии, корректива скорости либо коэффициента Кориолиса. Физический смысл этой величины будет раскрыт позже.
носит название коэффициента кинетической энергии, корректива скорости либо коэффициента Кориолиса. Физический смысл этой величины будет раскрыт позже.
Разделив обе части (9.16) на ускорение свободного падения g, выразим это соотношение в единицах длины, т.е. в форме напоров
 (9.17)
(9.17)

|
Рассмотрим движение потока вязкой жидкости в канале (рис. 9.2) от сечения 1-1 к сечению 2-2. Обозначим удельную энергию потока в сечении 1-1 через  , а в 2-2 -
, а в 2-2 -  .
.
| Рис. 9.2 |
Так как жидкость вязкая, то процесс ее перемещения сопровождается диссипацией энергии, т.е. какая-то ее часть расходуется на преодоление сил внутреннего трения и превращается в тепло, следовательно,  . Поэтому баланс энергии для выбранных сечений должен быть записан в виде
. Поэтому баланс энергии для выбранных сечений должен быть записан в виде
 (9.18)
(9.18)
где  - потери энергии.
- потери энергии.
Раскрывая значения  и
и  , получаем:
, получаем:
 (9.19)
(9.19)
Это и есть энергетическая форма уравнения Бернулли для потока вязкой жидкости.
В практических приложениях чаще используют уравнение Бернулли, выраженное в напорах
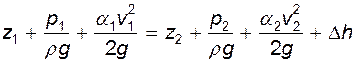 (9.20)
(9.20)
где  - потери напора.
- потери напора.
Для газовых потоков (без учета сжимаемости), а также при расчетах систем гидравлического привода обычно используют уравнение Бернулли в форме давлений
 (9.21)
(9.21)
где 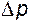 - потери давления.
- потери давления.
Обычно в упомянутых системах член 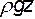 оказывается пренебрежимо малым по сравнению с остальными. В этих случаях (9.21) принимает вид:
оказывается пренебрежимо малым по сравнению с остальными. В этих случаях (9.21) принимает вид:
 (9.22)
(9.22)
Дата добавления: 2014-11-13; просмотров: 271; Мы поможем в написании вашей работы!; Нарушение авторских прав |