ЗАКОНОМЕРНОСТИ ЛАМИНАРНОГО РЕЖИМА ТЕЧЕНИЯ В КРУГЛЫХ ТРУБАХ.

При рассмотрении уравнений движения вязкой жидкости (уравнений Навье-Стокса) отмечалось, что интегрирование их в большинстве случаев связано с непреодолимыми математическими трудностями. Однако известны и исключения. К числу их относится ламинарное течение между параллельными пластинами, одна из которых движется с какой-то скоростью u. Это так называемое течение Куэтта.

Рассмотрение закономерностей этого течения можно найти в оригинально построенном современном американском курсе прикладной гидродинамики: Дейли Дж., Харлеман Д. Механика жидкости. -М.: Энергия, 1971. - 480 с.

Другим примером, интересующим нас в данном случае, является установившееся течение в круглой трубе, происходящее под действием постоянного перепада давлений - течение Пуазейля.

Профессор медицины Жан Пуазейль (1799-1869 гг.) во введении к своему трактату «Движение жидкостей в трубах малого диаметра» писал: «Я начал свои исследования потому, что прогресс в физиологии требовал определения законов движения жидкости в трубах малого диаметра (порядка 0,1 мм). Конечно, Дю Буа, Жирар, Навье и другие уже исследовали эти проблемы, однако они нуждаются в дальнейшем аналитическом и экспериментальном изучении, что было необходимо для надежного согласования теории с экспериментом». Опыты, выполненные Пуазейлем с трубкой диаметром 0,14 мм согласовывались с полученным им соотношением до тех пор, пока длина трубки составляла 51 мм; при уменьшении длины эта зависимость не соблюдалась. Этот факт и объясняется переходом от ламинарного к турбулентному режиму течения.

Как отмечалось выше, закономерности ламинарного течения в трубах можно получить путем прямого интегрирования уравнений Навье-Стокса. Решение задачи таким методом можно найти в книге: Аржаников Н.С., Мальцев В.Н. Аэродинамика. -М.: Изд-во оборонной промышл., 1956. -483 с.

В данном пособии мы воспользуемся другим способом, позво­ляющим получить более ясные физические представления.

Рассматриваем установившееся ламинарное течение в горизонтальной трубе, происходящее под действием постоянного перепада давления. Радиус трубопровода - R.

Двумя сечениями, отстоящими на расстоянии l друг от друга, выделим отсек трубопровода, и в нем цилиндр радиуса r. Составим уравнение движения. Так как течение установившееся, то сумма проекций на ось всех сил, действующих на цилиндр, должна быть равна нулю. Другими словами, активные силы, приводящие частицы жидкости в движение, должны быть равны силам сопротивления.

Активные силы: .

Силы сопротивления: .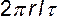

Таким образом, и

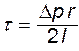(11.1)

Из (11.1), в частности, следует, что касательные напряжения изменяются вдоль радиуса по линейному закону. С другой стороны, по Ньютону касательные напряжения

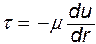(11.2)

Знак «минус» потому, что направления отсчета y и r противоположны.

Приравнивая (11.1) и (11.2), получаем

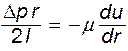(11.3)

Либо после разделения переменных

(11.4)

и после интегрирования

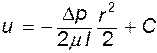(11.5)

Произвольную постоянную интегрирования находим из граничных условий: при 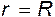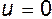(условие прилипания), и

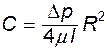
Следовательно,

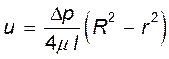(11.6)

либо

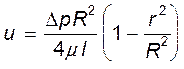(11.7)

Максимальная скорость движения частиц будет на оси трубы, т.е. при 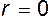, а ее величина

(11.8)

Подставляя (11.8) в (11.7) получим

(11.9)

Из чего следует, что в поперечном сечении трубы скорости распределены по параболическому закону, т.е. эпюра скорости представляет собой параболоид вращения.

Выражение (11.9) можно представить в виде

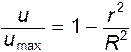(11.10)

Из чего следует, что отношение скорости в любой точке к скорости на оси не зависит от расхода, рода жидкости и материала стенок трубы: при всех значениях 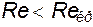оно одинаково.

Определим расход, протекающий через трубопровод. При введении понятия о средней скорости было показано, что

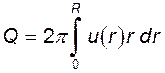(11.11)

где 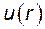- уравнение эпюры скорости.

Воспользуемся (11.6), что дает

(11.12)

Выполнив интегрирование и имея в виду (11.8), можно получить

Из чего следует, что

(11.13)

Раскрывая значение по (11.8), получаем выражение для определения потерь давления при ламинарном режиме течения в круглой трубе

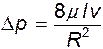(11.14)

Либо, заменяя радиус диаметром,

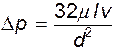(11.15)

Полученное соотношение носит название формулы Хагена-Пуазейля. Для потерь напора с учетом того, что 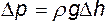, формула принимает вид

(11.16)

Важнейший вывод, следующий из этого соотношения, можно сформулировать так: потери давления (напора) при ламинарном течении в круглых трубах линейно зависят от средней скорости.

Выполним некоторые формальные преобразования формулы Хагена-Пуазейля, которые окажутся полезными в дальнейшем. Умножим числитель и знаменатель (11.16) на 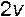, что дает

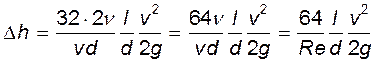(11.17)

Таким образом, можем записать, что в формуле при ламинарном течении .