КЛАССИФИКАЦИЯ ТЕЧЕНИЙ ЖИДКОСТИ. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ.

В 80-х годах XIX-го столетия работы, связанные с изучением сопротивления движению жидкости при течении в трубах, зашли в тупик. Опыты одних исследователей (немецкий инженер-строитель Г.Хаген, французский врач Ж.Пуазейль) показали, что сопротивление линейно зависит от скорости. В то же время не менее тщательные и точные опыты французского инженера А.Дарси свидетельствовали, что сопротивление пропорционально квадрату скорости. Возникшее противоречие тормозило развитие инженерной практики и требовало разрешения.

Наблюдения, выполненные Г.Хагеном еще в 1855 г. показали, что характер движения в трубе изменяется при достижении каких-то определенных условий. На это же со всей определенностью было указано в 1870 году нашим соотечественником проф. Н.Н.Петровым при разработке им теории гидродинамической смазки. Эта гипотеза нашла блестящее подтверждение в опытах английского физика Осборна Рейнольдса, результаты которых были опубликованы в 1883-1884 годах и имели далеко идущие последствия для всей механики жидкости.

Идея опытов отличалась ясностью и предельной простотой. В стеклянную трубу, скорость движения воды в которой могла регулироваться, Рейнольдс вводил струйки красителя. При малых скоростях струйки двигались параллельно оси трубы и вся картина представлялась неподвижной. При увеличении скорости воды за счет открытия крана картина изменялась, струйка красителя сначала приобретала синусоидальную форму, а дальнейшее увеличение скорости приводило к ее размыву, что свидетельствовало о беспорядочном движении.

Первый режим - спокойный, слоистый без перемешивания частиц был назван ламинарным. Второй - бурный, хаотичный, приводящий к перемешиванию частиц, позднее по предложению У. Томсона (Лорда Кельвина) получил название турбулентного. Как истинный ученый, Рейнольдс не остановился на констатации факта. Он предположил, что увеличении скорости потока приводит к возникновению каких-то возмущений, дестабилизирующих его структуру. Если понимать под устойчивостью способность потока подавлять возникающие в нем малые возмущения, то переход к турбулентному режиму может рассматриваться как потеря устойчивости. При этом из двух категорий сил, действующих на жидкие частицы, вязкого трения и инерции, первые играют стабилизирующую роль, а вторые - дестабилизирующую. Таким образом, отношение этих сил может служить критерием (мерой) устойчивости потока, т.е.

Мера устойчивости

Такой подход позволяет получить и количественную меру. Действительно, сила инерции . Массу можно представить как произведение плотности на объем, но объем пропорционален кубу линейных размеров, т. е. . Ускорение есть изменение скорости в единицу времени . Таким образом

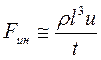(10.1)

По смыслу есть скорость, следовательно,

(10.2)

Сила вязкого трения (по Ньютону)

(10.3)

Действуя аналогично предыдущему, получаем

и безразмерный комплекс, характеризующий устойчивость, приобретает вид

(10.4)

В дальнейшем это соотношение получило название числа Рейнольдса, т.е.

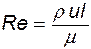(10.5)

где u - характерная скорость течения; l - характерный линейный размер.

Оригинальное толкование этого комплекса дано самим Рейнольдсом. Он писал: «Жидкость можно уподобить отряду воинов, ламинарное течение - монолитному походному строю, турбулентное - беспорядочному движению. Скорость жидкости - скорость отряда, диаметр трубы - величина отряда. Вязкость - дисциплина, а плотность - вооружение. Чем больше отряд, чем быстрее его движение и тяжелей вооружение, тем раньше распадается строй».

Для круглых труб характерный размер - диаметр, характерной скоростью является средняя скорость. С учетом этого, имея в виду, что , выражение (10.5) принимает вид

(10.6)

При течении в каналах некруглого сечения в качестве характерного размера принимают так называемый гидравлический радиус

(10.7)

где A - площадь поперечного сечения канала; - смоченный периметр (часть периметра, находящаяся в контакте с жидкостью).

Для круглых труб при напорном движении , и , т.е. гидравлический радиус в два раза меньше геометрического.

Одним из наиболее существенных результатов, обнаружен­ных в опытах Рейнольдса являлось то, что переход от ламинарного течения к турбулентному происходил при одном и том же численном значении введенного им критерия устойчивости, названного впоследствии критическим значением числа Рейнольдса ( ). По данным многочисленных опытов в круглых трубах . Это так называемое нижнее критическое число Рейнольдса, которое получают, если не принимать специальных мер по стабилизации потока. При принятии мер, переход к турбулентному течению можно существенно затянуть. При выполнении технических расчетов принято считать, что если число Рейнольдса, вычисленное по фактическим значениям параметров, меньше критического, то режим ламинарный, и наоборот.