Физический смысл коэффициента Кориолиса.

Как уже упоминалось, коэффициент носит название коэффициента кинетической энергии, корректива скорости, коэффициента Кориолиса. Выясним физический смысл этой величины.

Как уже отмечалось выше, второй член в уравнении (9.13) представляет собой кинетическую энергию секундной массы потока, определяемую истинным распределением скоростей в сечении, т.е.

(9.23)

Если бы скорости в сечении были бы распределены равномерно, то ( - средняя скорость потока), и кинетическая энергия потока была бы

(9.24)

Разделив (9.23) на (9.24), получим:

(9.25)

Следовательно, коэффициент Кориолиса представляет собой отношение кинетической энергии потока, вычисленной по истинному распределению скоростей, к кинетической энергии, определенной по средней скорости.

Для уяснения вопроса рассмотрим гипотетический «поток», состоящий из двух струек, скорости которых м/с и м/с и вычислим коэффициент Кориолиса.

Истинная кинетическая энергия (сумма кинетических энергий струек)

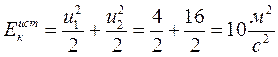
Средняя скорость ;

и , т. е. (истинная кинетическая энергия больше средней).

Легко убедится, что чем больше неравномерность распределения скоростей, тем больше коэффициент Кориолиса. Так, если м/с, а м/с, то . Очевидно, что минимальное значение 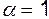будет при равномерном распределении скоростей. Действительно, пусть м/с, тогда и . Следовательно, можно утверждать, что корректирует ошибку, возникающую при вычислении кинетической энергии при замене истинного распределения скоростей условным равномерным.

Забегая несколько вперед, отметим, что в природе существует два принципиально отличающихся режима течения жидкости: ламинарный и турбулентный. При ламинарном течении в трубах , при турбулентном . Это позволяет утверждать, что в турбулентном потоке скорости в поперечном сечении распределены существенно равномерней, чем в ламинарном (эпюра турбулентного потока более «наполненная», ближе к прямоугольной по сравнению с эпюрой ламинарного потока).

Подведем некоторые итоги. Использование струйной модели потока и сведение его к одномерному путем введения представления о средней скорости позволяют получить одно из основных уравнений гидродинамики - уравнение Бернулли для потока вязкой жидкости. Принципиально, с помощью этого уравнения можно рассчитать движение жидкости в каналах при установившемся течении и условии, что в выбранных сечениях поток слабодеформированный либо параллельно-струйный. Однако, для полного решения задачи необходимо уметь определять потери напора ( 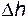), возникающие при движении жидкости в каналах. Эта далеко не простая задача и будет являться предметом дальнейшего рассмотрения.