ОСНОВЫ ТЕОРИИ ПОДОБИЯ И МОДЕЛИРОВАНИЯ

При рассмотрении различных разделов, связанных с движением жидких сред, неоднократно приходилось сталкиваться с процессами и явлениями, которые в силу своей сложности не позволяют получить аналитические решения, необходимые для инженерной практики. Вместе с тем переход от качественных суждений к количественным соотношениям играет ведущую роль в творческой деятельности человека.

Рассматриваемые в настоящем пособии вопросы непосредст­венно связаны с методологией научного познания. Однако, этот аспект, безусловно важный с познавательных позиций, далеко выходит за рамки курса, поэтому в настоящем пособии мы ограничимся лишь технической стороной.

Принципиально, процесс познания человеком природы можно условно разделить на две стадии: анализ и синтез. На первой стадии, т.е. на стадии анализа, изучаемый объект мысленно расчленяется на более простые составные части, выделяются свойства и связи.

На этапе синтеза происходит их соединение с целью воссоздания единого целого. Этап завершается построением математичес­кой модели, которая с какой-то степенью приближения описывает поведение изучаемого объекта. Обычно математическая модель представляет систему либо системы дифференциальных уравнений. Что же касается степени приближения модели, то она обусловлена теми упрощающими предпосылками, которые положены в основу. Здесь важную роль играет так называемый фактор неопределенности. Суть его сводится к тому, что с усложнением математической модели за счет более полного учета влияющих факторов уменьша­ется возможность получения точного, имеющего практическое значение представления. Другими словами, неопределенность решения возрастает по мере углубленного анализа реальной задачи.

Так, например, система дифференциальных уравнений Эйлера для гидродинамики является математической моделью, описывающей движение идеальной жидкости. Усложнение модели за счет учета сил вязкого трения приводит к системе дифференциальных уравнений Навье-Стокса.

Если модель разрешима, т.е. уравнения могут быть проинтегрированы любым путем, то можно считать, что решена и поставленная конкретная задача. Полученные результаты сопоставляются с теми, что наблюдаются в природе. Если они близки, то это означает, что модель правильно отражает поведение и свойства реального объекта, если нет, нужно ввести какие-то дополнительные факторы, не учтенные ранее, т.е. улучшить ее. Все это, конечно, не означает, что этот процесс идет легко и просто. Он может быть связан с преодолением огромных трудностей как математического, так и вычислительного характера. Новые проблемы возникают в двух случаях: несмотря на все усилия уравнения, составляющие математическую модель, проинтегрировать не удается; изучаемое явление оказыва­ется столь сложным, что не поддается математическому описанию.

В качестве примера первого случая можно привести уравнения Навье-Стокса, которые не могут быть проинтегрированы для большинства важных для практики случаев. Очевидно, что единст­венным в этих условиях способом решения задачи является эксперимент на физической модели, под которой понимается уменьшенный (либо увеличенный) реальный объект исследования. При этом сразу возникают три вопроса: как спроектировать и построить модель, какие величины необходимо измерять при проведении опытов, и как перенести результаты опытов, полученных на модели на натурный объект. На эти вопросы и отвечает теория подобия, являющаяся основой современного физического эксперимента. Прежде чем приступить к в ее рассмотрению, необходимо уяснить, что же понимается под подобием? Одно из наиболее удачных определений этого понятия принадлежит академику Л.И.Седову: «Подобными называются такие явления (процессы), когда по характеристикам одного из них можно получить характеристики другого простым пересчетом, аналогичным переходу от одной системы единиц к другой».

В общем случае различают три вида подобия: геометрическое, кинематическое и динамическое. Наиболее простым является подобие геометрическое, требующее, чтобы линейные размеры натуры и модели находились в постоянном соотношении, другими словами, модель повторяет натуру в каком-то масштабе.

Это требование можно записать в виде

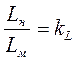
где - масштабный множитель.

Для площадей (S) и объемов (V)

;

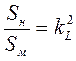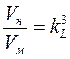
Можно отметить, что правила геометрического подобия были известны еще Джонотану Свифту, который отмечал, что в стране, в которую попал Гулливер в одном из своих путешествий, он обнаружил существа, превосходившие его по росту в 12 раз, по площади - в 144 раза и по объему - в 1728 раз.

Применительно к физическим явлениям элементарные представления геометрического подобия расширяются и распространяются на все величины, характеризующие данный процесс. Если учесть, что они могут изменяться как во времени, так и в прост­ранстве, образуя поля, то возникает понятие о временном подобии и подобии полей, называемое кинематическим подобием.

В механике жидкости оно сводится к подобию полей скоростей в потоках, движущихся в геометрически подобных каналах.

И наконец, имея в виду, что механическое движение происходит под действием сил, вводится понятие динамического подобия, которое требует, чтобы в соответствующих точках натуры и модели силы находились в постоянном соотношении.

Рассмотрим простейший пример. Известно, что движение любой механической системы подчиняется закону Ньютона

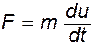(13.1)

Для двух подобных систем можно записать

и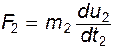

Разделив первое на второе получим:

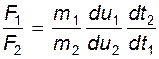либо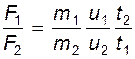

Имея в виду, что имеем

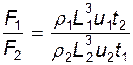
По смыслу есть скорость, поэтому

(13.2)

либо

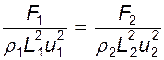(13.3)

Очевидно, что полученные комплексы безразмерны.

Таким образом, для двух подобных систем сохраняется числовое равенство безразмерных комплексов 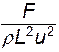. Кратко это условие можно записать так: . В честь Ньютона этот комплекс обозначается двумя первыми буквами его фамилии, т.е.

(13.4)

и называют числом подобия Ньютона, а выражение 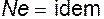- основным законом динамического подобия механических систем (законом Ньютона).

Величины L и u, входящие в (13.4), называются определяющим линейным размером и определяющей скоростью. При проведении опытов они выбираются экспериментатором произвольно, исходя из удобства их измерения.

Полученные результаты заслуживают того, чтобы остановиться и сделать кое-какие полезные выводы. Во-первых, они поз­воляют ответить на один из поставленных выше вопросов: как спроектировать и построить модель. Ответ очевиден: так, чтобы она была геометрически подобна натуре.

Во-вторых, из сказанного следует, что для обеспечения динамического подобия не требуется, чтобы все величины, определяющие характер процесса в натурном объекте, были численно равны аналогичным величинам в модели. Достаточным является равенство безразмерных комплексов, составленных из этих величин для натуры и модели, называемых числами подобия.

Какие преимущества дает такой подход в практическом плане?

Из математической статистики известно, что число опытов, которое необходимо поставить для того, чтобы получить закономерность, достоверно описывающую какое-то физическое явление, определяется из соотношения:

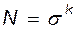(13.5)

где 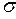- число экспериментальных точек, которое необходимо снять для обеспечения представительности опыта ( 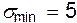); k - число величин, подлежащих варьированию в опытах.

Таким образом, минимальное число опытов

(13.6)

Если в опытах варьируется число Ньютона (например, за счет изменения скорости), то и 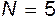, но если изучать влияние каждой из величин ( 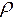, u, L), то 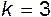и число опытов 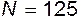. Следовательно, использование числа подобия в качестве своеобразной «обобщенной переменной» позволяет уменьшить число необходимых опытов в 25 раз, а если для надежности принять , то в 100 раз.

И наконец, в-третьих, можно ответить на вопрос о том, какие величины следует измерять в опытах и как переносить результаты на натурный объект. Так как при проведении опытов необходимо обеспечить равенство чисел подобия натуры и модели, то ясно, что измерению подлежат лишь те величины, которые входят в эти числа.

По результатам измерений можно вычислить числа подобия модели и, исходя из равенства их числам подобия натуры, произвести пересчет.

Остается открытым вопрос, который, по существу, является центральным. Как же найти числа подобия, характеризующие изу­чаемый процесс либо явление? Очевидно, что только ответ на него открывает путь для практической реализации теории подобия.