Потери давления (напора) при турбулентном течении в трубах.

Напомним, что рассмотрение закономерностей как ламинарного, так и турбулентного течений в трубах помимо чисто познавательных целей преследовало и цели сугубо практические: получить соотношения, позволяющие определять потери давления (напора) в трубопроводных сетях при выполнении инженерных расчетов. Для ламинарного течения эта задача решается с помощью формулы Хагена-Пуазейля. Из рассмотрения закономерностей турбулентного течения становится ясным, что вследствие его чрезвычайной сложности получение аналогичного соотношения чисто теоретическим путем практически невозможно. Поэтому, основываясь на уже известных положениях, установим хотя бы общую структуру необходимой формулы.

Как было показано, выражение для турбулентных касательных напряжений (напряжений Рейнольдса) имеет вид

Это с большой долей уверенности позволяет утверждать, что существует связь между средней скоростью и касательным напряжением на стенке трубы вида

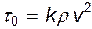(12.24)

где k - коэффициент пропорциональности.

С другой стороны, из условия равновесия движущегося под действием постоянного перепада давления жидкого цилиндра длиной l (см. 12.19)

После замены радиуса диаметром и подстановки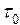

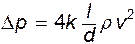(12.25)

либо

(12.26)

В такой форме записи выражение 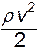имеет четкий физический смысл. Это так называемое динамическое давление потока, обусловленное средней скоростью, либо кинетическая энергия потока, заключенная в единице объема.

Обозначим величину и назовем ее гидравлическим коэффициентом трения, тогда

(12.27)

либо

(12.28)

Полученное соотношение носит название формулы Дарси. Более строго это соотношение будет получено методом анализа размернос­тей.

Отметим попутно, что если в преобразованной формуле Хагена-Пуазейля (см. 11.17) обозначить величину 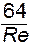буквой , то она превращается в формулу Дарси. В этом смысле формула Дарси может быть названа универсальной, т.е. пригодной как для ламинарного, так и для турбулентного течений. В последнем случае открытым остается вопрос о нахождении гидравлического коэффициента трения, который, как следует из всего сказанного выше, может быть решен только экспериментальным путем.

В заключение отметим, что хотя поставленная главная проб­лема и оказалась теоретически неразрешимой, полученные результаты позволяют найти решения ряда частных задач, имеющих важное практическое значение.