Анализ размерностей.

Следует подчеркнуть, что конечная цель в рассматриваемом случае остается прежней: нахождение чисел подобия, по которым следует вести моделирование, но решается она при существенно меньшем объеме информации о характере процесса.

Для уяснения дальнейшего кратко рассмотрим некоторые основополагающие понятия. Обстоятельное изложение можно найти в книге А.Н.Лебедева «Моделирование в научно-технических исследованиях». - М.: Радио и связь. 1989. -224 с.

Любой материальный объект обладает рядом свойств, которые допускают количественное выражение. При этом каждое из свойств характеризуется размером определенной физической величины. Единицы некоторых физических величин можно выбирать произвольно, и с их помощью представлять единицы всех остальных. Физические единицы, выбираемые произвольно, называют основными. В международной системе (применительно к механике) это - килограмм, метр и секунда. Остальные величины, выраженные через эти три, называют производными.

Основная единица может обозначаться либо символом соответствующей величины, либо специальным символом. Например, единицы длины - L, единицы массы - M, единица времени - T. Либо, единица длины - метр (м), единица массы - килограмм (кг), единица времени - секунда (с).

Под размерностью понимают символическое выражение (иногда его называют формулой) в виде степенного одночлена, связывающее производную величину с основными. Общий вид этой закономерности имеет вид

(13.11)

где x, y, z- показатели размерности.

Например, размерность скорости

Для безразмерной величины все показатели , и, следовательно, .

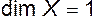Два следующих утверждения достаточно ясны и не нуждаются в каких-либо специальных доказательствах.

Отношение размеров двух объектов является величиной постоянной вне зависимости от того, в каких единицах они выражаются. Так, например, если отношение площади, занимаемой окнами, к площади стен составляет 0,2, то этот результат останется неизменным, если сами площади выражать в мм2, м2или км2.

Второе положение можно сформулировать следующим образом. Любое правильное физическое соотношение должно быть размерностно однородным. Это означает, что все члены, входящие как в правую, так и в левую его части должны иметь одинаковую размерность. Это простое правило четко реализуется в житейском обиходе. Все осознают, что метры можно складывать только с метрами и никак не с килограммами или с секундами. Нужно четко представлять, что правило остается справедливым и при рассмотрении даже самых сложных уравнений.

Метод анализа размерностей базируется на так называемой -теореме (читается: пи-теорема). -теорема устанавливает связь между функцией, выраженной через размерные параметры, и функцией в безразмерной форме. Более полно теорема может сформулирована так:

Любая функциональная зависимость между размерными величинами может быть представлена в виде зависимости между N безразмерными комплексами (числами ), составленными из этих величин. Число этих комплексов , где n - число основных единиц. Как уже отмечалось выше, в гидромеханике (кг, м, с).

Пусть, например, величина А является функцией пяти размерных величин ( 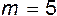), т.е.

(13.12)

Из -теоремы следует, что эта зависимость может быть преобразована в зависимость, содержащую два числа ( )

(13.13)

где и - безразмерные комплексы, составленные из размерных величин.

Эту теорему иногда приписывают Бэкингему и называют -теоремой Бэкингема. В действительности в её разработку внесли вклад многие крупные ученые, в том числе Фурье, Рябушинский, Рэлей.

Доказательство теоремы выходит за рамки курса. При необходимости оно может быть найдено в книге Л.И.Седова «Методы подобия и размерностей в механике» - М.: Наука, 1972. - 440 с. Подробное обоснование метода приводится и в книге В.А.Веникова и Г.В.Веникова «Теория подобия и моделирования» - М.: Высшая шко­ла, 1984. -439 с. Особенностью этой книги является то, что помимо вопросов, связанных с подобием, в нее включены сведения о методике постановки эксперимента и обработки его результатов.

Использование анализа размерностей для решения конкретных практических задач связано с необходимостью составления функциональной зависимости вида (13.12), которая на следующем этапе обрабатывается специальными приемами, приводящими в конечном итоге к получению чисел (чисел подобия).

Основным, носящим творческий характер, является первый этап, так как получаемые результаты зависят от того, насколько правильно и полно представление исследователя о физической природе процесса. Другими словами, насколько функциональная зависимость (13.12) правильно и полно учитывает все параметры, влияющие на изучаемый процесс. Любая ошибка здесь неизбежно приводит к ошибочным выводам. В истории науки известна так называемая «ошибка Рэлея». Суть ее в том, что изучая задачу о теп­лообмене при турбулентном течении, Рэлей не учел влияние вязкости потока, т.е. не включил её в зависимость (13.12). В результате в конечные соотношения, полученные им, не вошло число подобия Рейнольдса, играющее исключительно важную роль в теплообмене.

Для уяснения сущности метода рассмотрим пример, иллюст­рирующий как общий подход к задаче, так и способ получения чисел подобия.

Необходимо установить вид зависимости, позволяющий определить потери давления либо напора при турбулентном течении в круглых трубах.

Напомним, что эта задача уже рассматривалась в разделе 12.6. Поэтому представляет несомненный интерес установить, как она может быть разрешена с помощью анализа размерностей и дает ли это решение какую-то новую информацию.

Ясно, что падение давления вдоль трубы, обусловленное затратами энергии на преодоление сил вязкого трения обратно пропорционально её длине, поэтому с целью сокращения числа переменных целесообразно рассматривать не , а , т.е. потери давления на единицу длины трубы. Напомним, что отношение , где 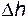- потери напора, носит название гидравлического уклона.

Из представлений о физической сущности процесса можно предположить что возникающие потери должны зависеть: от средней скорости течения рабочей среды (v); от размера трубопровода, определяемого его диаметром (d); от физических свойств транспортируемой среды, характеризуемых её плотностью ( 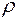) и вязкостью ( ); и, наконец, разумно считать, что потери должны быть как-то связаны с состоянием внутренней поверхностью трубы, т.е. с шероховатостью (k) ее стенок. Таким образом, зависимость (13.12) в рассматриваемом случае имеет вид

либо

(13.14)

На этом и заканчивается первый и, нужно подчеркнуть, наиболее ответственный этап анализа размерностей.

В соответствии с -теоремой, число влияющих параметров, входящих в зависимость, . Следовательно, число безразмерных комплексов 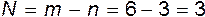, т.е. после соответствующей обработки (13.14) должна принять вид

(13.15)

Существует несколько способов нахождения чисел . Мы воспользуемся методом, предложенным Рэлеем.

Основным достоинством его является то, что он представляет собой своеобразный алгоритм, приводящий к решению задачи.

Из параметров, входящих в (13.15) необходимо выбрать три любых, но так, чтобы в них входили основные единицы, т.е. метр, килограмм и секунда. Пусть ими будут v, d, 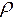. Легко убедиться, что они удовлетворяют поставленному требованию.

Образуются числа в виде степенных одночленов из выбранных параметров, умноженных на один из оставшихся в (13.14)

; (13.16)

; (13.17)

; (13.18)

Теперь задача сводится к нахождению всех показателей степеней. При этом они должны быть подобраны так, чтобы числа были безразмерны.

Для решения этой задачи определим прежде всего размерности всех параметров:

; ;

Вязкость , т.е. .

Параметр , и .

И, наконец, .

Таким образом, размерности чисел будут

либо

Аналогично два других

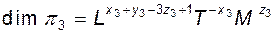
В начале раздела 13.3 уже отмечалось, что для любой безразмерной величины показатели размерности . Поэтому, например, для числа можем записать

Приравнивая показатели степеней, получаем три уравнения с тремя неизвестными

Откуда находим ; ; .

Подставляя эти значения в ( 13.6), получаем

(13.19)

Действуя аналогично, легко показать, что

и .

Таким образом, зависимость (13.15) принимает вид

(13.20)

Так как есть неопределяющее число подобия (число Эйлера), то (13.20) можно записать как функциональную зависимость

либо

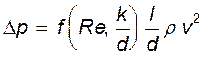(13.21)

Следует иметь в виду, что анализ размерностей не дает и принципиально не может дать каких-то числовых значений в получаемых с его помощью соотношениях. Поэтому он должен завершаться анализом результатов и при необходимости их корректировкой, исходя из общих физических представлений. Рассмотрим с этих позиций выражение (13.21). В правую его часть входит квадрат скорости, но эта запись не выражает ничего, кроме того, что скорость возводится в квадрат. Однако, если поделить эту величину на два, т.е. , то как известно из гидромеханики, она приобретает важный физический смысл: удельной кинетической энергии, а - динамическое давление, обусловленное средней скоростью. С учетом этого (13.21) целесообразно записать в виде

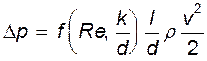(13.22)

Если теперь, как в (12.26), обозначить 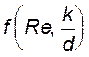буквой , то приходим к формуле Дарси

(13.23)

либо

(13.24)

где - гидравлический коэффициент трения, который, как следует из (13.22), является функцией числа Рейнольдса и относительной шероховатости (k/d). Вид этой зависимости может быть найден только экспериментальным путем.

ЛИТЕРАТУРА

1.Кальницкий Л.А., Добротин Д.А., Жевержеев В.Ф. Специальный курс высшей математики для втузов. М.:Высшая школа, 1976. - 389с.

2.Астарита Дж., Марручи Дж. Основы гидромеханики неньютоновских жидкостей. - М.: Мир, 1978.-307с.

3.Федяевский К.К., Фаддеев Ю.И. Гидромеханика. - М.: Судостроение, 1968. - 567 с.

4.Фабрикант Н.Я. Аэродинамика. - М.: Наука, 1964. - 814 с.

5.Аржаников Н.С. и Мальцев В.Н. Аэродинамика. - М.: Оборонгиз, 1956 - 483 с.

6.Фильчаков П.Ф. Приближенные методы конформных отображений. - К.: Наукова думка, 1964. - 530 с.

7.Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. - М.: Наука, 1987. - 688 с.

8.Дейли Дж., Харлеман Д. Механика жидкости. -М.: Энергия, 1971. - 480 с.

9.А.С. Монин , А.М. Яглом «Статистическая гидромеханика» (ч.1. -М.: Наука, 1968. -639 с.)

10.Шлихтинг Г. Теория пограничного слоя. - М.: Наука, 1974. - 711 с.

11.Павленко В.Г. Основы механики жидкости. - Л.: Судостроение, 1988. - 240 с.

12.Альтшуль А.Д. Гидравлические сопротивления. - М.: Недра, 1970. - 215 с.

13.А.А.Гухман «Введение в теорию подобия». - М.: Высшая школа, 1963. - 253 с.

14.С. Клайн «Подобие и приближенные методы». - М.: Мир, 1968. - 302 с.

15.А.А.Гухман «Применение теории подобия к исследованию процессов тепломассообмена. Процессы переноса в движущейся среде». - М.: Высшая шкала,1967. - 302 с.

16.А.Н.Лебедев «Моделирование в научно-технических исследованиях». - М.: Радио и связь. 1989. -224 с.

17.Л.И.Седов «Методы подобия и размерностей в механике» - М.: Наука, 1972. - 440 с.

18.В.А.Веников и Г.В.Веников «Теория подобия и моделирования» - М.: Высшая шко­ла, 1984. -439 с.

ОГЛАВЛЕНИЕ

1. МАТЕМАТИЧЕСКИЙ АППАРАТ, ИСПОЛЬЗУЕМЫЙ В МЕХАНИКЕ ЖИДКОСТИ................................................................................................ 3

1.1. Векторы и операции над ними................................................... 4

1.2. Операции первого порядка (дифференциальные характеристики поля). ......................................................................................................... 5

1.3. Операции второго порядка........................................................ 6

1.4. Интегральные соотношения теории поля.................................. 7

1.4.1. Поток векторного поля.................................................. 7

1.4.2. Циркуляция вектора поля.............................................. 7

1.4.3. Формула Стокса............................................................. 7

1.4.4. Формула Гаусса-Остроградского.................................. 7

2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА И ПАРАМЕТРЫ ЖИДКОСТИ. СИЛЫ И НАПРЯЖЕНИЯ........................................................................... 8

2.1. Плотность.................................................................................... 8

2.2. Вязкость....................................................................................... 9

2.3. Классификация сил.................................................................... 12

2.3.1. Массовые силы............................................................. 12

2.3.2. Поверхностные силы.................................................... 12

2.3.3. Тензор напряжения...................................................... 13

2.3.4. Уравнение движения в напряжениях........................... 16

3. ГИДРОСТАТИКА................................................................................. 18

3.1. Уравнение равновесия жидкости.............................................. 18

3.2. Основное уравнение гидростатики в дифференциальной форме. ......................................................................................................... 19

3.3. Эквипотенциальные поверхности и поверхности равного давления. ......................................................................................................... 20

3.4. Равновесие однородной несжимаемой жидкости в поле сил тяжести. Закон Паскаля. Гидростатический закон распре­деления давления... 20

3.5. Определение силы давления жидкости на поверхности тел.... 22

3.5.1. Плоская поверхность.................................................... 24

4. КИНЕМАТИКА..................................................................................... 26

4.1. Установившееся и неустановившееся движение жидкости...... 26

4.2. Уравнение неразрывности (сплошности)................................. 27

4.3. Линии тока и траектории.......................................................... 29

4.4. Трубка тока (поверхность тока)............................................... 29

4.5. Струйная модель потока........................................................... 29

4.6. Уравнение неразрывности для струйки................................... 30

4.7. Ускорение жидкой частицы...................................................... 31

4.8. Анализ движения жидкой частицы........................................... 32

4.8.1. Угловые деформации................................................... 32

4.8.2. Линейные деформации................................................. 36

5. ВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ.............................................. 38

5.1. Кинематика вихревого движения............................................. 38

5.2. Интенсивность вихря................................................................ 39

5.3. Циркуляция скорости............................................................... 41

5.4. Теорема Стокса......................................................................... 42

6. ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ ЖИДКОСТИ................................ 44

6.1. Потенциал скорости.................................................................. 44

6.2. Уравнение Лапласа................................................................... 46

6.3. Циркуляция скорости в потенциальном поле.......................... 47

6.4. Функция тока плоского течения............................................... 47

6.5. Гидромеханический смысл функции тока................................ 49

6.6. Связь потенциала скорости и функции тока............................ 49

6.7. Методы расчета потенциальных потоков................................ 50

6.8. Наложение потенциальных потоков......................................... 54

6.9. Бесциркуляционное обтекание круглого цилиндра................ 58

6.10. Применение теории функций комплексного переменного к изучению плоских потоков идеальной жидкости............................................ 60

6.11. Конформные отображения..................................................... 62

7. ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ............................. 65

7.1. Уравнения движения идеальной жидкости.............................. 65

7.2. Преобразование Громеки-Лэмба............................................. 66

7.3. Уравнение движения в форме Громеки-Лэмба........................ 67

7.4. Интегрирование уравнения движения для установившегося течения ......................................................................................................... 68

7.5. Упрощенный вывод уравнения Бернулли............................... 69

7.6. Энергетический смысл уравнения Бернулли........................... 70

7.7. Уравнение Бернулли в форме напоров.................................... 71

8. ГИДРОДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ..................................... 72

8.1. Модель вязкой жидкости.......................................................... 72

8.1.1. Гипотеза линейности ................................................... 72

8.1.2. Гипотеза однородности................................................ 74

8.1.3. Гипотеза изотропности................................................. 74

8.2 Уравнение движения вязкой жидкости. (уравнение Навье-Стокса) ......................................................................................................... 74

9. ОДНОМЕРНЫЕ ТЕЧЕНИЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ (основы гидравлики)........................................................................................................... 77

9.1. Расход потока и средняя скорость........................................... 77

9.2. Слабодеформированные потоки и их свойства....................... 78

9.3. Уравнение Бернулли для потока вязкой жидкости................. 79

9.4. Физический смысл коэффициента Кориолиса......................... 82

10. КЛАССИФИКАЦИЯ ТЕЧЕНИЙ ЖИДКОСТИ. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ.............................................................................................. 84

11. ЗАКОНОМЕРНОСТИ ЛАМИНАРНОГО РЕЖИМА ТЕЧЕНИЯ В КРУГЛЫХ ТРУБАХ..................................................................................................... 86

12. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ТУРБУЛЕНТНОГО ДВИЖЕНИЯ. .................................................................................................................. 90

12.1. Общие сведения....................................................................... 90

12.2. Уравнения Рейнольдса............................................................ 92

12.3. Полуэмпирические теории турбулентности.......................... 93

12.4. Турбулентное течение в трубах............................................. 95

12.5. Степенные законы распределения скоростей....................... 100

12.6. Потери давления (напора) при турбулентном течении в трубах. ......................................................................................................... 100

13. ОСНОВЫ ТЕОРИИ ПОДОБИЯ И МОДЕЛИРОВАНИЯ............... 102

13.1. Инспекционный анализ дифференциальных уравнений..... 106

13.2. Понятие об автомодельности................................................ 110

13.3. Анализ размерностей............................................................ 111

Литература …………………………………………………………………..118