
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 7. Оценка статистических характеристик результатов эксперимента, определение точности полученных результатов.
Для определения вероятностных характеристик погрешностей используются исходные данные, полученные предварительно опытным путем, посредством физического эксперимента. Результаты эксперимента в виде выборки некоторого объема n обрабатывают методами математической статистики и таким образом получают оценочные характеристики погрешностей.
Познакомимся с вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.
Каждый эксперимент содержит элемент неопределенности вследствие ограниченности экспериментального материала. Постановка повторных (или параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и нужно оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в одинаковых условиях несколько раз и затем берется среднее арифметическое всех результатов. Среднее арифметическое 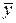 равно сумме всех m отдельных результатов, деленной на количество параллельных опытов
равно сумме всех m отдельных результатов, деленной на количество параллельных опытов
 (7.1)
(7.1)
Отклонение результата любого опыта от среднего арифметического можно представить как разность 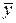 – у, где у – результат отдельного опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений повторных опытов. Для измерения этой изменчивости чаще всего используют дисперсию. Дисперсией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозначается D и выражается формулой
– у, где у – результат отдельного опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений повторных опытов. Для измерения этой изменчивости чаще всего используют дисперсию. Дисперсией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозначается D и выражается формулой
 (7.2)
(7.2)
где (m – 1) – число степеней свободы, равное количеству опытов минус единица. Одна степень свободы использована для вычисления среднего.
Корень квадратный из дисперсии, взятый с положительным знаком, называется средним квадратическим отклонением, стандартом или квадратичной ошибкой
 . (7.3)
. (7.3)
Стандарт имеет размерность той величины, для которой он вычислен. Дисперсия и стандарт – это меры рассеяния, изменчивости. Чем больше дисперсия и стандарт, тем больше рассеяны значения параллельных опытов около среднего значения.
Критерии исключения грубых ошибок. Ошибка опыта является суммарной величиной, результатом многих ошибок: ошибок измерений факторов, ошибок измерения функции отклика и др. Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.
Все ошибки принято разделять на случайные, систематические и промахи. Систематические ошибки находят, калибруя измерительные приборы и сопоставляя опытные данные с изменяющимися внешними условиями, при сравнении с эталонным прибором. Если систематические ошибки вызываются внешними условиями (переменной температуры, и т. д.), следует компенсировать их влияние. Случайными ошибками называются те, которые появляются нерегулярно, причины возникновения которых неизвестны и которые невозможно учесть заранее. При повторении опытов такие ошибки могут вызвать большой разброс экспериментальных результатов.
Очень важно исключить из экспериментальных данных грубые ошибки. Грубая погрешность, или промах, – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором. К ним можно отнести:
· неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
· неправильная запись результата наблюдений, значений отдельных мер использованного набора, например гирь;
· хаотические изменения параметров питающего средства измерений (СИ) напряжения, например его амплитуды или частоты.
Причинами грубых погрешностей могут быть внезапные и кратковременные изменения условий измерения и оставшиеся незамеченными неисправности в аппаратуре. Если промахи обнаруживают в процессе измерений, то результаты их содержащие отбрасывают. Однако чаще всего промахи выявляют при статистической обработке результатов измерений с помощью специальных критериев.
Корректная статистическая обработка выборки возможна только при ее однородности, т.е. в том случае, когда все ее члены принадлежат к одной и той же генеральной совокупности. В противном случае обработка данных бесмысленна. “Чужие” отсчеты по своим значениям могут существенно не отличаться от “своих” отсчетов. Их можно обнаружить только по виду гистограмм или дифференциальных законов распределения. Наличие таких аномальных отсчетов принято называть загрязнениями выборки, однако выделить члены выборки, принадлежащие каждой из генеральных совокупностей, практически невозможно.
Если “свои” и “чужие” отсчеты различаются по значениям, то их исключают из выборки. Особую неприятность доставляют отсчеты, которые хотя и не входят в компактную группу основной массы отсчетов выборки, но и не удалены от нее на значительное расстояние, – так называемые предполагаемые промахи. Отбрасывание “слишком” удаленных от центра выборки отсчетов называется “цензурированием” выборки. Это осуществляется с помощью специальных критериев.
При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения проводят два-три раза и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для обнаружения промахов используют статистические критерии, предварительно определив, какому виду распределения соответствует результат измерений.
Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения xi не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают.
Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.
Критерий “трех сигм” применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q £ 0,003, маловероятен и его можно считать промахом, если  , где Sy – оценка СКО измерений. Величины
, где Sy – оценка СКО измерений. Величины 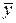 и Sy вычисляют без учета экстремальных значений yi. Данный критерий надежен при числе измерений n ³ 20… 50.
и Sy вычисляют без учета экстремальных значений yi. Данный критерий надежен при числе измерений n ³ 20… 50.
Это правило обычно считается слишком жестким, поэтому рекомендуется [5] назначать границу цензурирования в зависимости от объема выборки: при 6 < n £ 100 она равна 4Sy; при 100 < n £ 1000 – 4,5Sy; при 1000 < n £ 10000 – 5Sy. Данное правило применимо только для нормального закона.
Вариационный критерий Диксона. Этот критерий очень удобен и достаточно мощен (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд y1, y2, …, yn (y1< y2 < …< yn). Критерий Диксона определяется как KD=(yn– yn-1)/ (yn– y1). Критическая область для этого критерия P(KD>Zq) = q. Значения Zq приведены в таблице 6.
Таблица 6. Значения критерия Диксона.
| n | Zq при q, равном | |||
| 0,10 | 0,05 | 0,02 | 0,01 | |
| 0,68 0,48 0,40 0,35 0,29 0,28 0,26 0,26 0,22 | 0,76 0,56 0,47 0,41 0,35 0,33 0,31 0,30 0,26 | 0,85 0,64 0,54 0,48 0,41 0,39 0,37 0,36 0,31 | 0,89 0,70 0,59 0,53 0,45 0,43 0,41 0,39 0,34 |
Существуют и другие критерии исключения грубых ошибок [5], например, критерии Граббса, Шовене, Шарлье, Романовского.
Дисперсия воспроизводимости параллельных опытов. При планировании физического эксперимента определяются точки xi (  ) в факторном пространстве, в которых определяется экспериментальное значение функции отклика. Так как функция отклика y имеет случайный характер, то в каждой точке xi проводятся m повторных опытов, и дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов. По терминологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии воспроизводимости эксперимента.
) в факторном пространстве, в которых определяется экспериментальное значение функции отклика. Так как функция отклика y имеет случайный характер, то в каждой точке xi проводятся m повторных опытов, и дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов. По терминологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии воспроизводимости эксперимента.
В каждой точке результаты наблюдений  ,
,  , ... ,
, ... ,  усредняются:
усредняются:
 . (7.5)
. (7.5)
С целью оценки ошибки воспроизводимости в каждом опыте, состоящем из m повторных наблюдений, подсчитываются дисперсия  и стандарт
и стандарт  по формулам:
по формулам:
 ; (7.6)
; (7.6)
 , (7.7)
, (7.7)
где (m–1) – число степеней свободы, равное количеству повторных опытов, минус единица;  – среднее арифметическое, определяемое по формуле (7.5).
– среднее арифметическое, определяемое по формуле (7.5).
Если дисперсии Di (  ), вычисленные по формулам (7.6) однородны, то можно вычислить средневзвешенную дисперсию с суммарным числом степеней свободы. Такая дисперсия является значительно более надежной оценкой дисперсии воспроизводимости, чем отдельные выборочные дисперсии. Однородность дисперсий означает, что среди всех суммируемых дисперсий нет таких, которые бы значительно превышали все остальные.
), вычисленные по формулам (7.6) однородны, то можно вычислить средневзвешенную дисперсию с суммарным числом степеней свободы. Такая дисперсия является значительно более надежной оценкой дисперсии воспроизводимости, чем отдельные выборочные дисперсии. Однородность дисперсий означает, что среди всех суммируемых дисперсий нет таких, которые бы значительно превышали все остальные.
Для проверки однородности дисперсий  , полученных по выборкам одинакового объема m, используется критерий Кохрэна, который определяется отношением максимальной дисперсии к сумме всех дисперсий
, полученных по выборкам одинакового объема m, используется критерий Кохрэна, который определяется отношением максимальной дисперсии к сумме всех дисперсий
 . (7.8)
. (7.8)
С критерием Кохрэна связаны числа степеней свободы n1=m – 1 и n2 = N. Гипотеза об однородности дисперсией подтверждается, если экспериментальное значение критерия Кохрэна не превышает табличного значения (Приложение 2).
В случае однородности дисперсий можно усреднять дисперсии и для подсчета дисперсии воспроизводимости эксперимента с числом степеней свободы nвос=N (m – 1) пользоваться формулой
 (7.9)
(7.9)
Такой формулой можно пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.
На практике часто приходится сталкиваться со случаями, когда число повторных опытов различно. Это происходит вследствие отброса грубых наблюдений, неуверенности экспериментатора в правильности некоторых результатов (в таких случаях возникает желание еще и еще раз повторить опыт) и т. п.
Тогда при усреднении дисперсий приходится пользоваться средним взвешенным значением дисперсий, взятым с учетом числа степеней свободы
 (7.10)
(7.10)
где 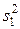 – дисперсия первого опыта,
– дисперсия первого опыта,  – дисперсия второго опыта и т. д., ν1 – число степеней свободы в первом опыте, равное числу параллельных опытов m минус 1, т. е. ν1= m1–1; ν2 – число степеней свободы во втором опыте и т. д. Число степеней свободы средней дисперсии принимается равным сумме чисел степеней свободы дисперсий, из которых она вычислена.
– дисперсия второго опыта и т. д., ν1 – число степеней свободы в первом опыте, равное числу параллельных опытов m минус 1, т. е. ν1= m1–1; ν2 – число степеней свободы во втором опыте и т. д. Число степеней свободы средней дисперсии принимается равным сумме чисел степеней свободы дисперсий, из которых она вычислена.
После исключения из повторных опытов грубых ошибок во всех опытах необходимо снова проверить однородность дисперсий  .
.
Отметим, что повторные опыты нельзя путать с повторными измерениями в одном опыте. Такие измерения часто делаются и являются полезными, но не могут заменить повторных опытов.
Определение закона распределения результатов измерений или случайных погрешностей измерений. При определении закона распределения случайных погрешностей измерений переходят от выборки результатов измерений y1, y2, y3, …, yn к выборке отклонений от среднего арифметического результатов измерений Δy1, Δy2, Δy3, …, Δyn, где Δ yi = yi – 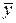 .
.
Первым шагом при идентификации закона распределения является построение по результатам измерения yi, i=1, 2, …, n, вариационного ряда (упорядоченной выборки). В вариационном ряду результаты измерения располагают в порядке возрастания. Далее этот ряд разбивают на оптимальное число r, как правило одинаковых интервалов длиной  .
.
Далее определяют число попаданий mi (частоты) результатов измерений в интервалы группирования. В рассматриваемом интервале отношение частоты mi к общему числу n измерений определяет частность
 (7.11)
(7.11)
или оценочную вероятность появления соответствующего результата измерения. Частоту появления результата измерения можно графически представить в виде гистограммы, т.е. ступенчатой диаграммы оценки p* плотности вероятности распределения результатов измерения по размеру. Частота pi соответствует площади i-го прямоугольника, а оценку плотности вероятности получают делением частости (площади) на интервал h (основание):
 (7.12)
(7.12)
При увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более приближается к гладкой кривой – графику плотности распределения вероятности.
По виду построенной гистограммы может быть оценен закон распределения результатов измерений.
Принято считать, что в большинстве тщательно поставленных экспериментов ошибки с хорошим приближением подчинены нормальному закону распределения
 , (7.13)
, (7.13)
где е – основание натурального логарифма, px(x) – плотность распределения вероятности. Теоретически это утверждение обосновывается исходя из центральной предельной теоремы теории вероятностей, которая утверждает, что сумма многих независимых источников погрешностей с произвольными функциями распределения асимптотически имеет нормальное распределение, если только ни одна из этих погрешностей не является превалирующей.
В результате получим следующий график:

При числе наблюдений n > 50 для проверки гипотезы о нормальности закона распределения случайной величины часто используют критерий согласия c2. Идея этого метода состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенных на основе нормального закона распределения.
Для этого критерия мерой отклонения статистического распределения случайной величины от нормального закона служит величина
c2 =  , (7.14)
, (7.14)
где mi – экспериментальные значения частот в интервалах разбиения [xi, xi+1]; n – число интервалов разбиения;  – теоретические вероятности попадания результатов наблюдения в интервалы разбиения.
– теоретические вероятности попадания результатов наблюдения в интервалы разбиения.
Величина ck2 подчиняется c2 распределению с k степенями свободы. Для нормального распределения число степеней свободы определяют по формуле k = m – 3.
Методика проверки соответствия принятого и экспериментального законов распределения заключается в следующем:
· определяются среднее арифметическое значение 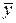 измеряемой величины по формуле (7.1) и среднеквадратическое отклонение результата измерения sy по формуле (7.3);
измеряемой величины по формуле (7.1) и среднеквадратическое отклонение результата измерения sy по формуле (7.3);
· группируются результаты наблюдений по интервалам длиной h, число которых определяется так же, как и при построении гистограммы;
· вычисляется число наблюдений для каждого из интервалов, теоретически соответствующее нормальному закону распределения. Для этого сначала от реальных середин интервалов yi0 переходят к нормированным серединам  . Затем для каждого значения zi с помощью аналитической модели находят функции плотности вероятности по формуле
. Затем для каждого значения zi с помощью аналитической модели находят функции плотности вероятности по формуле

По найденному значению f(zi) определяют ту часть Ni имеющихся наблюдений, которая теоретически должна быть в каждом из интервалов  , где n – общее число наблюдений.
, где n – общее число наблюдений.
· если в какой-либо интервал теоретически попадает меньше пяти наблюдений, то в обеих гистограммах его соединяют с соседним интервалом. После этого определяют число степеней свободы ν = m – 3, где m – общее число интервалов. Если было произведено укрупнение интервалов, то m – общее число интервалов после укрупнения;
· по формуле (7.14) определяют эмпирическое значение величины χ2;
· выбирают уровень значимости критерия q. Он должен быть небольшим, чтобы была мала вероятность совершить ошибку первого рода. При заданном уровне значимости q и числу степеней свободы ν находят границу критической области  , такую что
, такую что  = q. Вероятность того, что полученное значение χ2 превышает
= q. Вероятность того, что полученное значение χ2 превышает  , равна q и мала. Поэтому, если оказывается
, равна q и мала. Поэтому, если оказывается  , то гипотеза о нормальности закона распределения опытных данных принимается, т.е. она правдоподобна и не противоречит опытным данным с доверительной вероятностью p =1– q. В противном случае гипотеза отвергается, как противоречащая опытным данным.
, то гипотеза о нормальности закона распределения опытных данных принимается, т.е. она правдоподобна и не противоречит опытным данным с доверительной вероятностью p =1– q. В противном случае гипотеза отвергается, как противоречащая опытным данным.
Дата добавления: 2014-11-13; просмотров: 534; Мы поможем в написании вашей работы!; Нарушение авторских прав |