Глава 9. Обобщение методов вычисления размерных коэффициентов аналитических моделей объектов и систем на многофакторный эксперимент.

Допустим, что проведенный эксперимент имеет r факторов и что функция отклика и факторы связаны линейно:

y_i = b₀ + b₁x _i1 + ... + b_r x_ir + ε_i, . (9.1)

В случае многих переменных более удобной оказывается матричная форма записи всех необходимых в данной задаче соотношений. Введем следующие матрицы:

;

; .

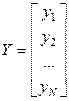Здесь Х – матрица факторов (условий опыта); Y– вектор столбец значений функции отклика; B – вектор столбец коэффициентов. Тогда систему (9.1) можно записать в матричном виде: Х В = Y.

Система нормальных уравнений МНК для определения коэффициентов для модели вида (9.1) имеет вид:

, (9.2)

где или в матричной форме

U = (Y – XB)^T(Y – XB). (9.3)

Минимум функции, если он существует, достигается при одновременном равенстве нулю частных производных по всем переменным.

Дифференцируя выражение (9.3) по переменным b_i (i = 1, 2, …, r) в соответствии с правилами матричного дифференцирования линейных и квадратичных функций получим

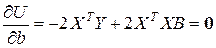, (9.4)

где 0 – вектор-столбец размерности r+1, состоящий из нулей,

.

Разрешая систему уравнений (9.4) относительно B получим систему уравнений в нормальном виде:

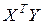= , (9.5)

где X^T – матрица условий опыта (факторов ) транспонирования по отношению к матрице Х. Матрица называется матрицей системы нормальных уравнений МНК.

Решим эту систему. Помножим правую и левую часть (9.5) на матрицу, обратную к матрице системы нормальных уравнений МНК:

В = (9.6)

Произведение прямой матрицы на обратную равно единичной матрице:

Е = (9.7)

Умножение вектора В на единичную матрицу Е его не изменяет и поэтому имеем выражение для определения коэффициентов в виде:

В = . (9.8)

Замечание. Поскольку вырожденная, сингулярная матрица (определитель, которой равен нулю) не имеет обратной, то решение системы нормальных уравнений возможно, если матрица системы невырождена, т.е. det 0.

Матрица системы нормальных уравнений МНК часто бывает вырожденной вследствие того, что факторы линейно связаны с другими независимыми переменными.

Необходимо отметить, что на практике бывают ситуации, когда линейные модели оказываются неадекватными, а переход к полиномам более высокого порядка невозможен ввиду плохой обусловленности матрицы нормальных уравнений, т.е. близости к нулю ее определителя. Это является нарушением четвертой предпосылки регрессионного анализа для нелинейных членов уравнения регрессии.

Для реализации метода множественной линейной регрессии в MATLAB используется функция B=regress(Y,X), вычисляющая вектор коэффициентов B в соответствии с формулой (9.8).