Порядок

проведения обработки результатов наблюдений.

Обработка ре зультатов многократных измерений должна проводиться в соответствии с ГОСТ 8.207.76 “ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения”

Исходной информацией для обработки является ряд из n (n > 4) результатов измерений y₁, y₂, y₃, …, y_n, из которых исключены известные систематические погрешности, – выборка.

Последовательность обработки результатов прямых многократных измерений состоит из ряда этапов.

1. Определение точечных оценок закона распределения результатов измерений.

На этом этапе определяются:

· среднее арифметическое значение 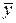измеряемой величины по формуле (7.1);

· среднеквадратическое отклонение результата измерения S_y по формуле (7.3);

В соответствии с рассмотренными выше критериями исключаются грубые погрешности, после чего проводится повторный расчет оценок среднее арифметического значения и его среднеквадратического отклонения.

2. Определение закона распределения результатов измерений или случайных погрешностей измерений. При числе наблюдений n>50 для идентификации закона распределения используется критерий Пирсона. При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий (d-критерий), приведенный в ГОСТ 8.207-76. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.

3. Определение доверительных границ случайной погрешности. Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находят квантильный множитель z_p при заданном значении доверительной вероятности P. В этом случае доверительные границы случайной погрешности Δ = .

4. Определение границ неисключенной систематической погрешности θ результата измерений [5].

5. Определение доверительных границ погрешности результата измерений Δ_р. Данная операция осуществляется путем суммирования среднеквадратического отклонения случайной составляющей 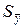и границ неисключенной систематической погрешности θ в зависимости от соотношения по правилам суммирования погрешностей [5].

6. Запись результата измерения. Результат измерения записывают в виде 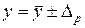при доверительной вероятности P = P_д.