
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Термодинамическая система.
Термодинамика имеет дело с термодинамической системой - совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией, как между собой, так и с другими телами (внешней средой).
Термодинамические системы, не обменивающиеся с внешней средой ни энергией, ни веществом, называются замкнутыми.
Основа термодинамического метода - определение состояния термодинамической системы.
Состояние системы задается термодинамическими параметрами (параметрами состояния) - совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и объем.
Параметры состояния системы могут изменяться. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом. Если для данной системы внешние условия не изменяются и
состояние системы с течением времени не меняется, то эта система находится в термодинамическом равновесии.
3.Температура.
Температура - одно из основных понятий, играющих важнейшую роль в физике в целом.
Температура - физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами.
В настоящее время используют две температурные шкалы.
Международная практическая шкала (шкала Цельсия ) градуированная в градусах Цельсия (°С) по двум реперным точкам - температурам замерзания и кипения воды при давлении 1,013∙105 Па, которые принимаются соответственно 0°С и 100°С.
Термодинамическая температурная шкала (шкала Кельвина), градуированная в градусах Кельвина (К) определяется по одной реперной точке - тройной точке воды - температуре, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии. Температура этой точки по данной шкале равна 273,16 К. Температура Т = 0 К называется нулем Кельвина.
Термодинамическая температура (Т) и температура (t) по Международной практической шкале связаны соотношением
Т = 273,15 +t.
Нормальные условия: Т0 =273,15 К = 0°С, р0 =101325 Па.
4.Идеальный газ.
Физическая модель, согласно которой:
• собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
• между молекулами газа отсутствуют силы взаимодействия;
• столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Исходя из этого идеальный газ можно рассматривать как совокупность беспорядочно движущихся молекул-шариков, имеющих пренебрежимо малый собственный объем и не взаимодействующих друг с другом на расстоянии.
Законы, описывающие поведение идеальных газов - законы Бойля- Мариотта, Авогадро, Дальтона, Гей-Люссака.
5.Закон Бойля-Мариотта.
Для данной массы газа m при постоянной температуре Т произведение давления р на объем V есть величина постоянная
 pV = const при Т = const и m = const.
pV = const при Т = const и m = const.
Кривая, изображающая зависимость между р и F, характеризующая свойства вещества при постоянной температуре, называется изотермой. Изотермы - гиперболы, расположенные на графике тем выше, чем выше температура происходящего процесса.
6.Закон Авогадро.
Количество вещества ν - физическая величина, определяемая числом специфических структурных элементов - молекул, атомов или ионов, из которых состоит вещество.
Единица количества вещества - моль - количество вещества системы, содержащей столько же структурных элементов, сколько содержится в 0,012 кг изотопа углерода 12С.
В одном моле различных веществ содержится одно и то же число молекул NA, называемое числом Авогадро. 
 Закон Авогадро:моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы.
Закон Авогадро:моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы.
При нормальных условиях (Т = Т0, р = р0) этот объем Vµ (молярный объем) равен 
Молярная масса µ=  - это масса одного моля вещества. Отсюда: v=
- это масса одного моля вещества. Отсюда: v= 
Единица молярной массы - килограмм на моль (кг/моль).
7.Закон Дальтона.
Парциальное давление - давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений р1,р2,...,рп входящих в нее газов:
Р = Р1+Р2+- + Рn или P= 
8.  Закон Гей-Люссака.
Закон Гей-Люссака.
1)Давление р данной массы m газа при постоянном объеме изменяется линейно с температурой t
р = р0(1+ αt), при V = const, m = const.
2)Объем V данной массы m газа при постоянном давлении изменяется линейно с температурой t
V = V0 (1 + α t), при р = const; m = const.
где а =  , V0 и р0 - объем и давление при
, V0 и р0 - объем и давление при
t = 0°С.
Процесс, протекающий при постоянном давлении, называется изобарным. На диаграмме в координатах (V,t) этот процесс изображается прямой, называемой изобарой.
Процесс, протекающий при постоянномобъеме, называется изохорным. На диаграмме в координатах (p,t) он изображается прямой, называемой изохорой. Изобары и изохоры пересекают ось температуры в точке t=-1/α=-273ºC . Если начало отсчета сместить в эту точку, то получим шкалу Кельвина (термодинамическую температуру) 
В термодинамической шкале температур: 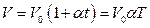

Откуда следует  или
или 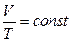 при
при 
 или
или  при
при  (закон Шарля),
(закон Шарля),
где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
9. Уравнение состояния идеального газа.
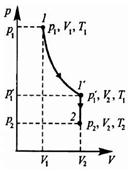 Уравнением состояния термодинамической системы называется уравнение, которое связывает давление р, объем V и температуру Т термодинамической системы, находящейся в состоянии термодинамического равновесия:
Уравнением состояния термодинамической системы называется уравнение, которое связывает давление р, объем V и температуру Т термодинамической системы, находящейся в состоянии термодинамического равновесия:
f(p,V,T) = О
где каждая из переменных является функцией двух других.
Пусть некоторая масса газа занимает объем Vx, имеет давление рх и находится при температуре Тх. Эта же масса газа в другом произвольном состоянии характеризуется параметрами p2,V2,T2. Переход из состояния 1 в состояние 2 осуществляется последовательно изотермическим (1-1') и изохорным (1'-2) процессами.
По законам Бойля-Мариотта и Гей-Люссака

Исключая  получим уравнение состояния идеального газа
получим уравнение состояния идеального газа
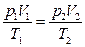 или
или 
По закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем  Уравнение состояния для моля идеального газа:
Уравнение состояния для моля идеального газа:  , где константа R = 8,31 Дж/(мольК) – называется универсальной газовой постоянной.
, где константа R = 8,31 Дж/(мольК) – называется универсальной газовой постоянной.
Объем газа массы m: V= v  =
= 
Отсюда 
Уравнение Менделеева-Клапейрона - уравнение состояния для массы т идеального газа

Если использовать постоянную Больцмана  то уравнение состояния примет вид
то уравнение состояния примет вид  где
где  концентрация молекул - число молекул в единице объема.
концентрация молекул - число молекул в единице объема.
Таким образом:
1)давление идеального газа при данной температуре прямо пропорционально концентрации его молекул,
2)при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул.
Число молекул, содержащихся в 1м3 газа при нормальных условиях, называется числом Лошмидта

10. Основное уравнение молекулярно-кинетической теории идеальных газов.
Пусть в сосуде объемом V находится идеальный газ массой т, состоящий из N молекул массой т0, движущихся с одинаковыми скоростями и. Концентрация молекул в газе по определению n = N/V.
Если при соударениях со стенками за время ∆t элементарной площадке ∆S стенки сосуда передается импульс ∆P, то давление газа, оказываемое им
на стенку сосуда 
При каждом соударении молекула, движущаяся перпендикулярно стенке, передает ей импульс 2  . В среднем по направлению к стенке движется
. В среднем по направлению к стенке движется  часть всех молекул. (Если рассмотреть три взаимно перпендикулярные оси, то в среднем только
часть всех молекул. (Если рассмотреть три взаимно перпендикулярные оси, то в среднем только  молекул движется вдоль одной из осей и только половина из них
молекул движется вдоль одной из осей и только половина из них  вдоль данного направления.) Поэтому, за время ∆t площадки ∆S достигнут
вдоль данного направления.) Поэтому, за время ∆t площадки ∆S достигнут  молекул и передадут ей импульс ∆P=
молекул и передадут ей импульс ∆P=  . Давление, оказываемое газом на стенку сосуда
. Давление, оказываемое газом на стенку сосуда 
Если газ в объеме V содержит N молекул, движущихся со скоростями υ1, υ2,…,υN, то целесообразно рассматривать среднюю квадратичную скорость, которая определяется как 
и характеризует всю совокупность молекул газа.
Основное уравнение молекулярно-кинетической теории идеальных газов

Другие варианты записи этого уравнения с учетом соотношений  и
и 

Здесь Е - суммарная кинетическая энергия поступательного движения всех молекул газа.- молярный объем,µ - молярная масса.
Используя уравнение Клапейрона-Менделеева, получим
 ,откуда
,откуда 
11.Средняя квадратичная скорость молекул идеального газа

где использовано  и
и 
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа

Отсюда следует, что  при Т=0К - прекращается движение молекул газа.
при Т=0К - прекращается движение молекул газа.
Молекулярно-кинетическое толкование температуры: термодинамическая температура - есть мера средней кинетической энергии поступательного движения молекул газа.
12. Закон Максвелла о распределении молекул идеального газа по скоростям.
 В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией f(υ), называемой функцией распределения молекул по скоростям, которая определяет относительное число молекул, скорости которых лежат в интервале от υ до υ+dυ т. е.
В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией f(υ), называемой функцией распределения молекул по скоростям, которая определяет относительное число молекул, скорости которых лежат в интервале от υ до υ+dυ т. е.

Закон Максвелла

Эта функция удовлетворяет условию нормировки.

13.Наиболее вероятная скорость молекул идеального газа.
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью  .
.
Приравняв  нулю, получаем:
нулю, получаем:

С повышением температуры  растет.
растет.
14. Средняя скорость молекулы газа (средняя арифметическая скорость).

15 Скорости, характеризующие состояние газа.

16.Барометрическая Формула.
В однородном поле тяготения Земли тепловое движение молекул приводит к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает. Давление на высоте h газа с молярной массой µ, относительно уровня моря, где давление р0 считается нормальным, равно.
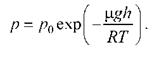
17.Распределение Больцмана.
Используя соотношения  ,
,  и
и  получаем выражение
получаем выражение 
Так как  - потенциальная энергия молекулы в поле тяготения, следовательно
- потенциальная энергия молекулы в поле тяготения, следовательно 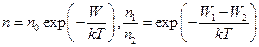
Такое распределение называют распределением Больцмана (распределение частиц по значениям потенциальной энергии) для внешнего потенциального поля.
Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
18.Средняя длина свободного пробега молекул.
Путь, который в среднем проходят молекулы между двумя последовательными столкновениями называется средней длиной свободного пробега молекул.
Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d.
Так как за 1с молекула проходит путь, равный средней арифметической скорости  , и если
, и если  - среднее число столкновений, испытываемых одной молекулой газа за 1с, то средняя длина свободного пробега
- среднее число столкновений, испытываемых одной молекулой газа за 1с, то средняя длина свободного пробега 
Можно показать, что  , откуда:
, откуда: 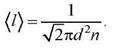
19.Эксперименты, подтверждающие молекулярно-кинетическую теорию.
1. Броуновское движение. Любые частицы малых размеров, взвешенные в газе или жидкости, совершают сложное зигзагообразное движение. Броуновское движение взвешенных частиц вызывается ударами молекул среды, в которой частицы взвешены. Подтверждение гипотезы о хаотическом тепловом движении молекул.
 2. Опыт Штерна. Два коаксиальных цилиндра синхронно вращаются в вакууме. Атомы серебра, испарясь с проволоки, расположенной вдоль оси внутреннего цилиндра, вылетают через щель и оседают на внутренней стенке наружного цилиндра. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.
2. Опыт Штерна. Два коаксиальных цилиндра синхронно вращаются в вакууме. Атомы серебра, испарясь с проволоки, расположенной вдоль оси внутреннего цилиндра, вылетают через щель и оседают на внутренней стенке наружного цилиндра. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.
3. Опыт Ламмерта. Между источником молекулярного пучка и приемником
 синхронно вращаются два диска с радиальными щелями. Из числа молекул, пролетевших через первую щель, пролетят через второй диск только те, которые подлетят к нему в тот момент, когда на пути пучка встанет прорезь во втором диске. Изменяя угловую скорость вращения, можно исследовать распределение молекул по скоростям.
синхронно вращаются два диска с радиальными щелями. Из числа молекул, пролетевших через первую щель, пролетят через второй диск только те, которые подлетят к нему в тот момент, когда на пути пучка встанет прорезь во втором диске. Изменяя угловую скорость вращения, можно исследовать распределение молекул по скоростям.
20.Явления переноса.
 Явлениями переноса называются необратимые процессы в термодинамически неравновесных системах, в которых происходит пространственный перенос энергии (теплопроводность), массы (диффузия), импульса (внутреннее трение).
Явлениями переноса называются необратимые процессы в термодинамически неравновесных системах, в которых происходит пространственный перенос энергии (теплопроводность), массы (диффузия), импульса (внутреннее трение).
Для простоты ограничимся одномерными случаями, выбрав ось х так, чтобы она была направлена в направлении переноса. Будем рассматривать потоки энергии, вещества и импульса упорядоченного движения частиц через единичную площадку (S= 1), перпендикулярную оси х, для идеального газа плотностью  , у которого
, у которого
 - средняя скорость теплового движения молекул,
- средняя скорость теплового движения молекул,
 - средняя длина свободного пробега.
- средняя длина свободного пробега.
21.Теплопроводность.
Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул - выравнивание температур.
Перенос энергии (в форме теплоты) описывается законом Фурье.
Здесь  - плотность теплового потока - тепловая энергия, переносимая в единицу времени через единичную площадку, перпендикулярную оси х,
- плотность теплового потока - тепловая энергия, переносимая в единицу времени через единичную площадку, перпендикулярную оси х, 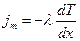
 - коэффициент теплопроводности,
- коэффициент теплопроводности, 
 - градиент температуры - скорость изменения температуры на единицу длины х в направлении нормали к этой площадке,
- градиент температуры - скорость изменения температуры на единицу длины х в направлении нормали к этой площадке,
 - удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К).
- удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К).
22.Диффузия.
Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену частицами (перенос масс) между этими телами, возникает и продолжается, пока существует градиент плотности.
Перенос массы (диффузия) для химически однородного газа подчиняется закону Фика.
Здесь  - плотность потока массы - масса вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х,
- плотность потока массы - масса вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, 
D - коэффициент диффузии, 
 - градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке.
- градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке.
23.Внутреннее трение (вязкость).
Вследствие хаотического теплового движения молекул происходит обмен молекулами между слоями газа движущимися с различными скоростями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее - увеличивается (происходит перенос импульса от одного слоя к другому). Это приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
Внутреннее трение описывается законом Ньютона.
Здесь 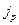 - плотность потока импульса– полный импульс, переносимый в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х,
- плотность потока импульса– полный импульс, переносимый в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, 
 - динамическая вязкость,
- динамическая вязкость,
 - градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев газа.
- градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев газа.
Внешнее сходство математических выражений, описывающих явления переноса, обусловлено общностью лежащего в основе явлений
теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения.
Формулы для коэффициентов 
 и
и  связывают коэффициенты
связывают коэффициенты
переноса и характеристики теплового движения молекул.
Соотношения между 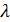 ,D и η: η=
,D и η: η= 
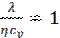
24.Внутренняя энергия термодинамической системы.
Внутренняя энергия U - это энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц.
К внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.
Внутренняя энергия - однозначная функция термодинамического состояния системы - в каждом состоянии система обладает вполне определенной внутренней энергией.
Поэтому, внутренняя энергия не зависит от того, каким образом система пришла в данное состояние.
При переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода.
25.Число степеней свободы.
Число степеней свободы - это число независимых переменных, полностью определяющих положение системы в пространстве.
Число степеней свободы для идеального газа жестких молекул.

В реальных молекулах нет жесткой связи между атомами в молекуле, поэтому необходимо учитывать также степени свободы колебательного движения атомов внутри молекулы.
Независимо от общего числа степеней свободы молекулы, три степени свободы всегда поступательные. На каждую из них приходится треть кинетической энергии поступательного движения молекулы 

Дата добавления: 2014-10-31; просмотров: 988; Мы поможем в написании вашей работы!; Нарушение авторских прав |