
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая работа № 1. Многочленная, кусочно-многочленная, сплайновая и обратная интерполяция
Для студентов специальности «Математическое обеспечение и администрирование информационных систем» отведено 4 часа практических занятий, а для студентов специальности «Программное обеспечение вычислительной техники и автоматизированных систем» - 2 часа.
План занятий:
1. Актуализация понятий обратимая и обратная функции, геометрического смысла обратимости, графика обратной функции, свойств таблицы значений обратимой и обратной функции, сплайн-функции.
2. Повторение постановок задач интерполяции с простыми и кратными узлами, интерполяционных формул Лагранжа, Ньютона и Эрмита, геометрического смысла интерполяции, оценок погрешности интерполяционных многочленов Лагранжа и Эрмита, кусочно-многочленной, сплайновой и обратной интерполяции.
3. Решение примеров.
4. Консультирование студентов по выполнению домашней работы.
Рассматриваемые примеры:
1. Дана таблица значений некоторой функции  .
.
| x | -1 | |||
| y | -1 |
Построить по ней интерполяционный многочлен 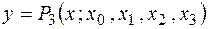 в форме Лагранжа и Ньютона. По этой же таблице провести обратную интерполяцию, то есть построить интерполяционный многочлен Ньютона
в форме Лагранжа и Ньютона. По этой же таблице провести обратную интерполяцию, то есть построить интерполяционный многочлен Ньютона 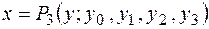 . Сравнить полученные результаты.
. Сравнить полученные результаты.
Решение:
Подставим в общую формулу для многочлена Лагранжа значения  (i=0,1,2,3) и приведем многочлен к стандартному виду.
(i=0,1,2,3) и приведем многочлен к стандартному виду.
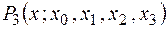

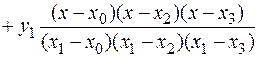


 0+
0+ 
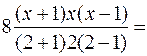







 .
.
Запишем многочлен Ньютона в общем виде:
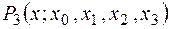



 .
.
Найдем соответствующие разделенные разности и запишем их в таблицу.
 ,
,  ,
,  ,
,  ,
,
 ,
,  .
.
| i | 
| 
| 
| 
| 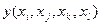
|
| -1 | -1 | ||||
Подставим в общую формулу значения  и разделенные разности:
и разделенные разности:

 .
.
Проведем обратную интерполяцию, для чего построим теперь интерполяционный многочлен  . Запишем его в общем виде:
. Запишем его в общем виде:
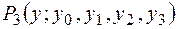
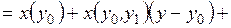

 .
.
Найдем разделенные разности и запишем их в таблицу.
 ,
,  ,
,  ,
,  ,
,
 ,
,  .
.
| i | 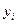
| 
| 
| 
| 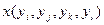
|
| -1 | -1 | ||||

| |||||

| |||||

| |||||
Подставим в общую формулу значения  и разделенные разности:
и разделенные разности:
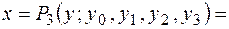
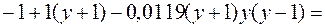

 .
.
Графики уравнений 
 ,
, 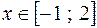 и
и  =
= 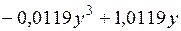 ,
, 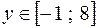 , очевидно, различны, но довольно близки. Близость графиков связана с тем, что график многочлена
, очевидно, различны, но довольно близки. Близость графиков связана с тем, что график многочлена  есть приближение для графика функции
есть приближение для графика функции  , а график уравнения
, а график уравнения  есть приближение для графика уравнения
есть приближение для графика уравнения  , совпадающего с графиком функции
, совпадающего с графиком функции  .
.
2. Дана таблица значений некоторой функции  и её производной:
и её производной:
| x | -1 | ||
| y | -1 | ||
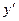
|
Построить по ней интерполяционный многочлен Эрмита 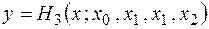 .
.
Решение:
Запишем многочлен Эрмита в общем виде:
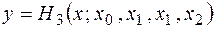 =
= 
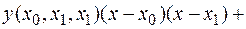
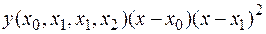 .
.
Найдем соответствующие разделенные разности и запишем их в таблицу.
 ,
, 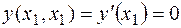 ,
,  ,
, 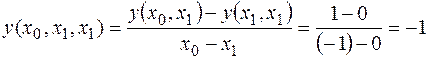 ,
,
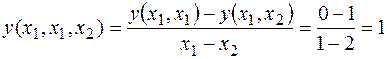 ,
,  .
.
| i | 
| 
| 
| 
| 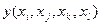
|
| -1 | -1 | ||||
| -1 | |||||
Подставим в общую формулу значения 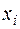 и разделенные разности. Получим:
и разделенные разности. Получим:
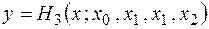 =
= 
 .
.
3. Дана функция  .
.  ,
,  . Строятся интерполяционный многочлен
. Строятся интерполяционный многочлен  и многочлен Эрмита
и многочлен Эрмита  , которые используются в качестве приближений этой функции. Найти оценки погрешности этих приближений в точке
, которые используются в качестве приближений этой функции. Найти оценки погрешности этих приближений в точке  .
.
Решение:
Оценка погрешности интерполяционного многочлена Лагранжа находится по формуле:
 .
.
Здесь  - верхняя граница
- верхняя граница 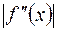 на
на 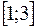 .
.
Оценка погрешности интерполяционного многочлена Эрмита находится по формуле:
 .
.
Здесь  - верхняя граница
- верхняя граница 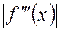 на
на 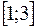 .
.
Для дальнейших вычислений найдем постоянные  и
и  . Для этого найдем производные функции:
. Для этого найдем производные функции:
 ,
,  ,
,  . Оценим модули старших производных на
. Оценим модули старших производных на 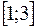 :
:

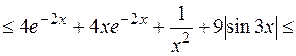

 .
.
Здесь использовано свойство модуля (модуль суммы не превышает суммы модулей), а также то, что на 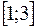 выполнено:
выполнено:  ,
,  ,
, 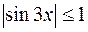 . Таким образом,
. Таким образом,  =14.
=14.

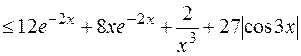

 . Здесь использовано также то, что
. Здесь использовано также то, что 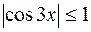 . Таким образом,
. Таким образом,  =38.
=38.
Теперь вычислим искомые оценки:
 ,
, 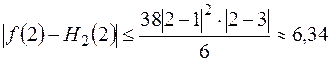 .
.
4. Дана функция  ,
,  . Отрезок
. Отрезок  делится на n равных частей точками
делится на n равных частей точками  . Вычисляются значения этой функции
. Вычисляются значения этой функции  ,
,  . По полученной таблице значений функции строится интерполяционный многочлен Лагранжа
. По полученной таблице значений функции строится интерполяционный многочлен Лагранжа  , который используется для приближения функции
, который используется для приближения функции  .
.
Составить алгоритм для вычисления значения y интерполяционного многочлена  по заданному значению x. Записать его на алгоритмическом языке.
по заданному значению x. Записать его на алгоритмическом языке.
Решение:
Исходные данные для алгоритма: функция  , число отрезков разбиения n, аргумент функции x, концы отрезка a и b. Результат: значение многочлена Лагранжа y. В алгоритме используются два цикла. Внешний цикл – для вычисления суммы, а внутренний – для вычисления произведения. Массив
, число отрезков разбиения n, аргумент функции x, концы отрезка a и b. Результат: значение многочлена Лагранжа y. В алгоритме используются два цикла. Внешний цикл – для вычисления суммы, а внутренний – для вычисления произведения. Массив 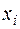 не вводится. Значения
не вводится. Значения  непосредственно подставляются в формулы.
непосредственно подставляются в формулы.
алг Интерполяционный многочлен (аргвещ x, a, b; цел n; резвещ y)
начцел i, j; вещ p, h
y:=0; 
нцдля i от 0 до n
p:=f(a+ih)
нцдля j от 0 до n
если i  j
j
то 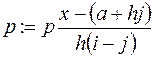
Все
Кц
y:=y+p
Кц
Кон
5. Дана функция  ,
,  . Отрезок
. Отрезок  делится на n равных частей точками
делится на n равных частей точками  . Вычисляются значения этой функции
. Вычисляются значения этой функции  ,
,  . По полученной таблице значений функции строится интерполяционный сплайн. Составить алгоритм для вычисления значения y интерполяционного сплайна по заданному значению x.
. По полученной таблице значений функции строится интерполяционный сплайн. Составить алгоритм для вычисления значения y интерполяционного сплайна по заданному значению x.
Решение:
Исходные данные для алгоритма: функция  , число отрезков разбиения n, аргумент функции x, концы отрезка a и b.
, число отрезков разбиения n, аргумент функции x, концы отрезка a и b.
Результат:
Значение интерполяционного сплайна y. Последовательность действий описана в теории. Запишем ее с учетом условия равномерности сетки точек 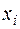 , из которой следует, что
, из которой следует, что  .
.
1. 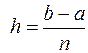 .
.
2.  ,
,  .
.
3.  ,
,  .
.
4. Решение следующей системы линейных алгебраических уравнений с трехдиагональной матрицей:
 ,
,
 ,
,  ,
,
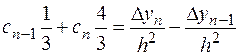 .
.
Эта система совпадет со стандартным видом системы, которая решалась методом прогонки, если n заменить на M,  заменить на
заменить на 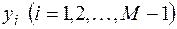 (не перепутайте их с величинами, вычисляемыми в пункте 2 нашего алгоритма). При этом
(не перепутайте их с величинами, вычисляемыми в пункте 2 нашего алгоритма). При этом
 ,
,  ,
,
 ,
,  .
.
Поэтому решать эту систему целесообразно методом прогонки.
В результате решения системы будут найдены величины 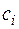
 .
.
5.  ,
,  .
.
6.  ,
,  .
.
7. 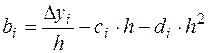 ,
,  .
.
8.  ,
,  .
.
9. Вычисление номера отрезка, которому принадлежит значение аргумента x:  .
.
10. Вычисление значения сплайна:
 .
.
Дата добавления: 2014-11-13; просмотров: 379; Мы поможем в написании вашей работы!; Нарушение авторских прав |