
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая работа № 4. Численное интегрирование
Для студентов специальности «Математическое обеспечение и администрирование информационных систем» отведено 6 часов практических занятий, а для студентов специальности «Программное обеспечение вычислительной техники и автоматизированных систем» - 2 часа.
План занятий:
1. Актуализация понятий неопределенного, определенного, несобственных и кратных интегралов, сходимости несобственных интегралов, свойств определенных и несобственных интегралов.
2. Повторение квадратурных формул Ньютона-Котеса, Гаусса, оценок погрешностей и порядков точности квадратурных формул.
3. Повторение метода повторного счета (правила Рунге)
4. Повторение первой и второй схем метода Монте-Карло.
5. Повторение алгоритма вычисления приближенных значений первообразной, методов приближенного вычисления несобственных и кратных интегралов.
6. Решение примеров.
7. Консультирование студентов по выполнению домашней работы.
Рассматриваемые примеры:
1. Для вычисления приближенного значения интеграла 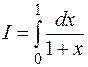 используется метод средних прямоугольников. Пользуясь оценкой погрешности для формулы средних прямоугольников, подобрать число отрезков разбиения n и шаг интегрирования h так, чтобы абсолютная погрешность приближенного значения интеграла не превышала
используется метод средних прямоугольников. Пользуясь оценкой погрешности для формулы средних прямоугольников, подобрать число отрезков разбиения n и шаг интегрирования h так, чтобы абсолютная погрешность приближенного значения интеграла не превышала  .
.
Решение:
Приближенное значение интеграла  вычисляется по следующей обобщенной формуле средних прямоугольников:
вычисляется по следующей обобщенной формуле средних прямоугольников: 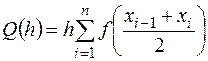 . Здесь n – заданное число отрезков разбиения,
. Здесь n – заданное число отрезков разбиения, 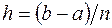 - шаг интегрирования,
- шаг интегрирования,  (
( 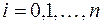 ) – узлы квадратуры.
) – узлы квадратуры.
Запишем оценку погрешности приближенного значения  :
:
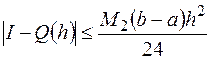 .
.
Здесь  - положительная постоянная, такая, что
- положительная постоянная, такая, что 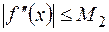 на
на  . В нашем случае
. В нашем случае  ,
,  ,
, 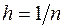 ,
, 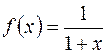 .
.
Найдем постоянную  . Для этого вычислим вторую производную подынтегральной функции:
. Для этого вычислим вторую производную подынтегральной функции: 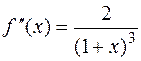 . Эта производная, очевидно, убывает на
. Эта производная, очевидно, убывает на 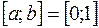 и положительна. Поэтому
и положительна. Поэтому 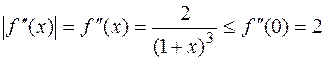 на
на  . Таким образом,
. Таким образом, 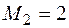 .
.
Учитывая это, оценку погрешности можно записать в виде: 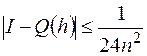 . Ее удобнее выражать через n.
. Ее удобнее выражать через n.
Значение n будем выбирать исходя из требования: 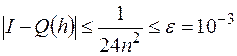 , обеспечивающего для приближенного значения интеграла заданную точность. Решим это неравенство относительно n:
, обеспечивающего для приближенного значения интеграла заданную точность. Решим это неравенство относительно n: 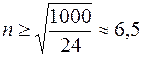 . Наименьшее целое значение n, удовлетворяющее этому неравенству, равно 7. Итак,
. Наименьшее целое значение n, удовлетворяющее этому неравенству, равно 7. Итак, 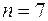 ,
, 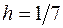 .
.
2. Составить алгоритм вычисления приближенного значения интеграла  методом Симпсона с погрешностью, не превышающей заданного положительного числа
методом Симпсона с погрешностью, не превышающей заданного положительного числа  . Значение m подбирается методом повторного счета с использованием асимптотической оценки погрешности по правилу Рунге. Записать алгоритм на алгоритмическом языке.
. Значение m подбирается методом повторного счета с использованием асимптотической оценки погрешности по правилу Рунге. Записать алгоритм на алгоритмическом языке.
Решение:
Исходными данными для алгоритма являются значения a, b,  и функция
и функция  . Приближенное значение интеграла вычисляется по формуле:
. Приближенное значение интеграла вычисляется по формуле:
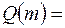
 .
.
Здесь 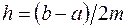 - шаг интегрирования,
- шаг интегрирования,  (
( 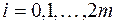 ) – узлы квадратуры. В обозначении приближенного значения интеграла
) – узлы квадратуры. В обозначении приближенного значения интеграла 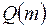 подчеркнута зависимость его от параметра m. Подставляя значения узлов, получим:
подчеркнута зависимость его от параметра m. Подставляя значения узлов, получим:
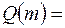
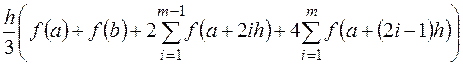 .
.
Значение параметра m подбирается методом повторного счета так, чтобы абсолютная погрешность 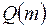 не превышала
не превышала  . При этом используется асимптотическая оценка погрешности по правилу Рунге
. При этом используется асимптотическая оценка погрешности по правилу Рунге
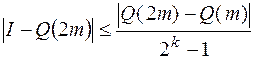 .
.
Здесь 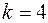 - порядок точности обобщенной формулы Симпсона.
- порядок точности обобщенной формулы Симпсона.
Метод повторного счета представляет собой цикл, в котором последовательно вычисляются значения 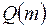 при
при 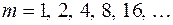 На каждом шаге этого цикла, начиная со второго, проверяется условие достижения заданной точности:
На каждом шаге этого цикла, начиная со второго, проверяется условие достижения заданной точности:
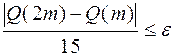 .
.
Как только это условие выполнится, цикл свою работу закончит и в качестве искомого приближенного значения интеграла выбирается последнее вычисленное значение  .
.
На каждом шаге цикла используются только два приближенных значения интеграла. Поэтому мы введем две переменные  и
и  , которые в цикле должны принимать попарно следующие значения:
, которые в цикле должны принимать попарно следующие значения:  =
= 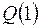 ,
,  =
= 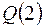 ;
;  =
= 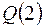 ,
,  =
= 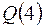 ;
;  =
= 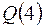 ,
,  =
= 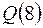 и так далее. Заметим, что значение
и так далее. Заметим, что значение  на всех шагах цикла, кроме первого, совпадает со значением
на всех шагах цикла, кроме первого, совпадает со значением  на предыдущем шаге цикла. Поэтому в цикле мы будем вычислять только значение
на предыдущем шаге цикла. Поэтому в цикле мы будем вычислять только значение  =
=  , а значение
, а значение  =
= 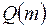 мы будем передавать с предыдущего шага цикла:
мы будем передавать с предыдущего шага цикла:  . Условие окончания цикла в этом случае примет вид:
. Условие окончания цикла в этом случае примет вид: 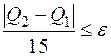 . Если используется цикл с постусловием, то для того, чтобы цикл мог начать работу, необходимо до цикла вычислить начальное значение:
. Если используется цикл с постусловием, то для того, чтобы цикл мог начать работу, необходимо до цикла вычислить начальное значение:
 =
= 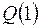 =
= 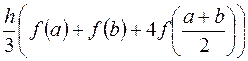 .
.
Введем в алгоритмический язык цикл с постусловием, аналогичный циклу repeat в языке Паскаль
Дата добавления: 2014-11-13; просмотров: 428; Мы поможем в написании вашей работы!; Нарушение авторских прав |