Нц повторять

Команды, повторяемые в цикле

кцпокане Условие окончания цикла

Запишем теперь алгоритм вычисления приближенного решения задачи Коши.

алг Метод Рунге-Кутта для 1 уравнения с автоматическим выбором шага (аргвещ a, b, , )

начвещ , ; цел n, N

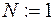| Задание начального значения параметра N

Метод Рунге-Кутта для 1 уравнения и с заданным шагом (a, b, , N, )

нцповторять | Начало цикла метода повторного счета

; | Передача значения с предыдущего шага

| цикла или начального значения.

; | Удвоение значения параметра N.

Метод Рунге-Кутта для 1 уравнения и с заданным шагом (a, b, , N, )

кцпокане | Конец цикла метода

| повторного счета

Кон

3. Составить алгоритм для вычисления приближённого решения задачи Коши для системы дифференциальных уравнений:

;

методом Рунге-Кутта четвертого порядка точности (число отрезков разбиения N считается заданным). Записать его на алгоритмическом языке.

Решение:

Исходными данными для алгоритма являются: N, m, a, b, , , … , , а также функции , , … , . Результаты: - приближенные значения . Здесь , , , .

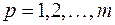Вычислительная схема метода Рунге-Кутта 4 порядка точности в координатах записывается в виде:

,

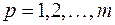
Так же, как и в алгоритме из первого примера, мы не будем использовать табличные переменные , . Для текущих расчетов мы введем простую переменную x и одномерный массив , а результаты будем записывать в файл вывода в следующей последовательности:

………

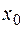
Кроме того, в качестве дополнительного результата в заголовке алгоритма используем массив z [1:m], такой, что . Это может понадобиться в дальнейшем при записи алгоритма повторного счета.

Для записи в файл значения любой величины p мы введем команду запись (p), а для перевода строки – команду перевод.

Значения мы будем брать из файла ввода. Они должны быть записаны в файл ввода до начала исполнения алгоритма в следующей последовательности:

.

Для чтения очередного значения из файла ввода и присвоения его переменной p мы введем команду чтение (p).

Чтобы описать множество функций c аргументом, мы введем функцию трех аргументов: , где - массив с m компонентами.

Запишем теперь алгоритм вычисления приближенного решения задачи Коши.

алг Метод Рунге-Кутта для m уравнений и с заданным шагом (аргвещ a, b, цел m, цел N, резвещтаб )

начвещ x, h, вещтаб , , ,

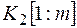, ; цел n, p

x:=a; ;

нцдля p от 1 до m

чтение ; | Чтение из файла ввода начальных

| данных:

Кц

запись(x); перевод | Запись в файл вывода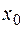

нцдля p от 1 до m

запись( ) | Запись в файл вывода

Кц

перевод

нцдля n от 0 до N-1 | Начало цикла метода Рунге-Кутта

нцдля p от 1 до m

|

Кц

|

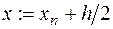
нцдля p от 1 до m

|

Кц

нцдля p от 1 до m

|

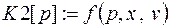
Кц

нцдля p от 1 до m

|

Кц

нцдля p от 1 до m

|

Кц

|

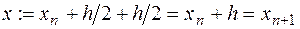
нцдля p от 1 до m

|

Кц

нцдля p от 1 до m

|

Кц

запись(x); перевод | Запись в файл вывода

нцдля p от 1 до m

|

запись( ) | Запись в файл вывода

|

Кц

перевод | Переменная x и массив u здесь уже

| приняли значения, необходимые для

| выполнения следующего шага цикла

кц | Конец цикла метода Рунге-Кутта.

нцдля p от 1 до m

|

Кц

Кон