
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая работа № 2. Наилучшее среднеквадратическое приближение. Тригонометрическая интерполяция. Наилучшее равномерное приближение
Для студентов специальности «Математическое обеспечение и администрирование информационных систем» отведено 6 часов практических занятий, а для студентов специальности «Программное обеспечение вычислительной техники и автоматизированных систем» - 3 часа.
План занятий:
1. Актуализация понятий тригонометрического ряда Фурье и его свойств, предгильбертова, нормированного и метрического пространства, аксиом скалярного произведения, нормы и метрики.
2. Повторение понятия ортогональности и ряда Фурье в гильбертовом пространстве, неравенства Бесселя и равенства Парсеваля.
3. Повторение формулы Родрига, многочленов Лежандра и разложения функции в ряд Фурье по системе ортогональных многочленов Лежандра.
4. Повторение общей схемы метода наименьших квадратов, полиномиальной и линейной аппроксимации.
5. Повторение способов линеаризации и их использования для поиска наилучших среднеквадратичных приближений в некоторых семействах нелинейных функций.
6. Повторение постановки задачи тригонометрической интерполяции, процедуры построения тригонометрического интерполяционного многочлена, понятия наилучшего равномерного приближения, теоремы Чебышева, способов построения наилучших равномерных приближений в семействах многочленов нулевого и первого порядка.
7. Решение примеров.
8. Консультирование студентов по выполнению домашней работы.
Рассматриваемые примеры:
1. Разложить в тригонометрический ряд Фурье функцию 
Изобразить график периодического (с периодом  ) продолжения функции
) продолжения функции  . Установить, к чему сходится ряд Фурье. Найти наилучшее среднеквадратическое приближение функции
. Установить, к чему сходится ряд Фурье. Найти наилучшее среднеквадратическое приближение функции  на
на  в множестве тригонометрических многочленов n-й степени
в множестве тригонометрических многочленов n-й степени
 .
.
Решение:
Найдем тригонометрический ряд Фурье для функции  . Функция определена на
. Функция определена на  . Поэтому мы воспользуемся формулами для ряда Фурье при
. Поэтому мы воспользуемся формулами для ряда Фурье при  :
:
 .
.
Вычислим коэффициенты Фурье:
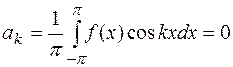 , поскольку подынтегральная функция нечетная, а интеграл берется в симметричных пределах.
, поскольку подынтегральная функция нечетная, а интеграл берется в симметричных пределах.

Здесь использовано, что  . Таким образом, разложение функции в тригонометрический ряд Фурье будет иметь вид:
. Таким образом, разложение функции в тригонометрический ряд Фурье будет иметь вид:
 .
.
 График периодического (с периодом
График периодического (с периодом  ) продолжения функции
) продолжения функции  изображен на рис. 1. Обозначим это продолжение
изображен на рис. 1. Обозначим это продолжение  . Согласно теореме 2, ряд Фурье будет сходиться к
. Согласно теореме 2, ряд Фурье будет сходиться к  во всех точках x из
во всех точках x из  , кроме точек
, кроме точек  ,
,  и
и  . В этих точках терпит разрыв первого рода периодическое продолжение
. В этих точках терпит разрыв первого рода периодическое продолжение  .
.
В точке  ряд Фурье будет сходиться к
ряд Фурье будет сходиться к  .
.
В точке  ряд Фурье будет сходиться к
ряд Фурье будет сходиться к 
В точке  ряд Фурье будет сходиться к
ряд Фурье будет сходиться к 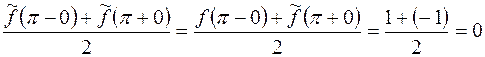 .
.
Наилучшим приближением для функции  в множестве тригонометрических многочленов n-й степени
в множестве тригонометрических многочленов n-й степени  является частичная сумма ряда Фурье:
является частичная сумма ряда Фурье:
 .
.
2. Найти наилучшее среднеквадратичное приближение функции 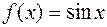 , определенной на отрезке
, определенной на отрезке  , в семействе многочленов вида
, в семействе многочленов вида  .
.
Решение:
Определим многочлены Лежандра до второго порядка по формуле Родрига:
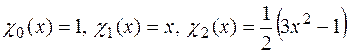 .
.
Найдем коэффициенты Фурье.
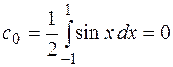 .
.
Здесь использовано, что подынтегральная функция нечетная, а интеграл берется в симметричных пределах.
 .
.
Вычислим сначала неопределенный интеграл:



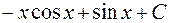 .
.
Продолжим вычисление  :
:


 .
.
 .
.
Здесь использовано, что подынтегральная функция нечетная, а интеграл берется в симметричных пределах.
Искомое приближение представляет собой частичную сумму ряда Фурье:

 .
.
3. Дана таблица значений  ,
,  некоторой функции
некоторой функции  . Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение функции в семействе многочленов 1-го порядка:
. Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение функции в семействе многочленов 1-го порядка: 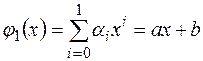 . Составить алгоритм для вычисления коэффициентов a и b этого приближения.
. Составить алгоритм для вычисления коэффициентов a и b этого приближения.
Решение:
Исходные данные для алгоритма: N, 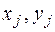
 . Результаты:
. Результаты:  ,
,  .
.
Вначале по формулам
 ,
,  ,
,  ,
,  ,
,
вычисляются величины  .
.
Далее проверяется условие
 .
.
Если оно выполняется, то вычисляются значения коэффициентов a и b по формулам

и строится график приближения и табличные точки. В противном случае строятся только табличные точки.
4. Дана таблица значений  ,
,  некоторой функции
некоторой функции  . Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение функции в семействе многочленов n-го порядка:
. Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение функции в семействе многочленов n-го порядка:  . Составить алгоритм для вычисления коэффициентов
. Составить алгоритм для вычисления коэффициентов  , а также для вычисления значений функции
, а также для вычисления значений функции 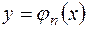 .
.
Решение:
Исходные данные для алгоритма: n, N, 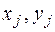
 . Результаты:
. Результаты: 
 .
.
Вначале вычисляются элементы матрицы и правой части системы
 .
.
Далее происходит обращение к алгоритму решения линейной системы методом Гаусса. С его помощью вычисляются 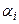
 , если матрица системы невырожденная. Если же матрица системы вырожденная, приближение не определяется.
, если матрица системы невырожденная. Если же матрица системы вырожденная, приближение не определяется.
На этом описание алгоритма можно было бы закончить, но есть две особенности, требующие пояснения. Стандартный алгоритм метода Гаусса применяется к решению линейных систем вида:  . Здесь
. Здесь  - порядок системы,
- порядок системы,  - элементы матрицы системы,
- элементы матрицы системы,  - компоненты правой части,
- компоненты правой части,  - компоненты решения. Наша система имеет другой вид, поскольку нумерация компонентов векторов и матриц там начинается с нуля, а не с 1. Для того чтобы привести нашу систему к нужному виду, сделаем сдвиг индексов, заменим везде в формулах i на i-1 , а p - на p-1. Новые индексы будут изменяться от 1 до n+1:
- компоненты решения. Наша система имеет другой вид, поскольку нумерация компонентов векторов и матриц там начинается с нуля, а не с 1. Для того чтобы привести нашу систему к нужному виду, сделаем сдвиг индексов, заменим везде в формулах i на i-1 , а p - на p-1. Новые индексы будут изменяться от 1 до n+1:
 .
.
Таким образом, перед обращением к алгоритму решения линейной системы методом Гаусса необходимо задать исходные данные для него в виде:  ,
,  ,
,  . Степени
. Степени  и
и  в программе лучше вычислять в виде произведений
в программе лучше вычислять в виде произведений  ,
,  , поскольку
, поскольку  могут быть отрицательными или равными 0, в то время как операция возведения в степень работает только для положительных аргументов. По окончании решения системы методом Гаусса мы получим
могут быть отрицательными или равными 0, в то время как операция возведения в степень работает только для положительных аргументов. По окончании решения системы методом Гаусса мы получим  . Значения искомых коэффициентов мы получим с помощью обратного сдвига индекса:
. Значения искомых коэффициентов мы получим с помощью обратного сдвига индекса:  .
.
При вычислении значений искомого приближения по формуле  лучше использовать алгоритмическую схему Горнера. Напомним ее. Требуется для заданного значения аргумента x вычислить соответствующее значение алгебраического многочлена
лучше использовать алгоритмическую схему Горнера. Напомним ее. Требуется для заданного значения аргумента x вычислить соответствующее значение алгебраического многочлена  с известными коэффициентами
с известными коэффициентами  . Для этого используется циклический алгоритм:
. Для этого используется циклический алгоритм:

нцдля l от n-1 до 0 с шагом (-1)

Кц
5. Дана таблица значений  ,
,  некоторой функции
некоторой функции  . Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение
. Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение 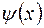 в семействе нелинейных функций
в семействе нелинейных функций  . Составить алгоритм для вычисления коэффициентов a и b этого приближения. Определить меру близости, в смысле которой это приближение будет наилучшим.
. Составить алгоритм для вычисления коэффициентов a и b этого приближения. Определить меру близости, в смысле которой это приближение будет наилучшим.
Решение:
Исходные данные для алгоритма: N, 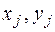
 . Результаты:
. Результаты:  ,
,  .
.
Вводятся новые переменные X и Y таким образом, чтобы после замены переменных функция  превращалась в линейную функцию:
превращалась в линейную функцию:

В результате этих замен мы получим линейную зависимость:
 .
.
На основании известных табличных данных  и
и  (
(  ) по формулам замен переменных находятся новые табличные данные
) по формулам замен переменных находятся новые табличные данные  и
и  для новой линейной зависимости:
для новой линейной зависимости:
 ,
,  .
.
По полученной новой таблице  методом наименьших квадратов подберем коэффициенты
методом наименьших квадратов подберем коэффициенты  ,
,  наилучшего линейного приближения
наилучшего линейного приближения 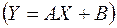 . Вначале вычисляются элементы матрицы и правой части соответствующей линейной системы:
. Вначале вычисляются элементы матрицы и правой части соответствующей линейной системы:
 ,
,  ,
, 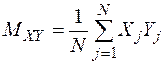 ,
,
 .
.
Далее проверяется условие существования и единственности решения этой системы  . Если оно выполняется, то вычисляются значения коэффициентов A и B по формулам:
. Если оно выполняется, то вычисляются значения коэффициентов A и B по формулам:

и получается само наилучшее линейное приближение 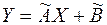 . Сравнивая это равенство с равенством
. Сравнивая это равенство с равенством  , получим соответствующие значения коэффициентов:
, получим соответствующие значения коэффициентов:  ,
,  . А в качестве искомого наилучшего нелинейного приближения выберем соответствующее приближение в первом параметрическом семействе функций
. А в качестве искомого наилучшего нелинейного приближения выберем соответствующее приближение в первом параметрическом семействе функций  . Это приближение будет наилучшим в смысле следующей нестандартной меры близости:
. Это приближение будет наилучшим в смысле следующей нестандартной меры близости:
 .
.
Если условие  не выполняется, то приближение не вычисляется.
не выполняется, то приближение не вычисляется.
6. Построить тригонометрический интерполяционный много-член второго порядка,  , для функции
, для функции  (здесь
(здесь  - целая часть вещественного числа x).
- целая часть вещественного числа x).
Решение:
Найдем табличные значения функции  на ее периоде. Наименьший период функции
на ее периоде. Наименьший период функции  равен
равен  . Порядок многочлена равен n=2, и, следовательно,
. Порядок многочлена равен n=2, и, следовательно,  . Получим узлы интерполяции на периоде:
. Получим узлы интерполяции на периоде:
 ,
, 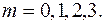
Отсюда  ,
,  ,
,  ,
,  . Так как все эти узлы принадлежат промежутку
. Так как все эти узлы принадлежат промежутку  , их целые части равны 0 и
, их целые части равны 0 и
 ,
, 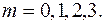
Следовательно, табличные значения функции  на ее периоде:
на ее периоде:
 ,
,  ,
,  ,
, 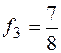 .
.
Запишем в общем виде искомый тригонометрический интерполяционный многочлен:

Вычислим коэффициенты этого многочлена по формулам:
 ,
,  ,
,
 ,
,  .
.
Запишем искомый тригонометрический интерполяционный многочлен
 .
.
7.Функция  приближается тригонометрическим интерполяционным многочленом 2-го порядка,
приближается тригонометрическим интерполяционным многочленом 2-го порядка,  . Найти оценку погрешности тригонометрической интерполяции.
. Найти оценку погрешности тригонометрической интерполяции.
Решение:
Функция  имеет наименьший период
имеет наименьший период  . Порядок тригонометрического многочлена n=2. Поэтому
. Порядок тригонометрического многочлена n=2. Поэтому  . Значение r может быть любым, так как функция
. Значение r может быть любым, так как функция  имеет ограниченные производные любого порядка. Поэтому мы не будем конкретизировать значение r. Легко показать, что для любого натурального k выполняется неравенство:
имеет ограниченные производные любого порядка. Поэтому мы не будем конкретизировать значение r. Легко показать, что для любого натурального k выполняется неравенство:  . Отсюда
. Отсюда  .
.
Подставим найденные значения в формулу оценки погрешности и получим искомую оценку погрешности тригонометрической интерполяции как функцию r:

Исследуем полученную оценку и попытаемся найти ее наименьшее значение. Величина r может иметь любое натуральное значение, а  . Поэтому абсолютная погрешность интерполяции,
. Поэтому абсолютная погрешность интерполяции,  , не может превышать любого положительного числа. Следовательно,
, не может превышать любого положительного числа. Следовательно, 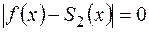 и
и  .
.
8. Построить для функции  многочлен наилучшего равномерного приближения нулевой степени,
многочлен наилучшего равномерного приближения нулевой степени,  , на
, на 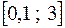 .
.
Решение:
Найдем  и
и  . Производная функции
. Производная функции  обращается в ноль в точке
обращается в ноль в точке  , принадлежащей нашему отрезку. На
, принадлежащей нашему отрезку. На  производная отрицательна, а на
производная отрицательна, а на  - положительна. Поэтому
- положительна. Поэтому
 .
.
Наибольшее значение функция  может принимать только на концах отрезка
может принимать только на концах отрезка 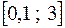 . Поэтому мы вычислим эти два значения функции и выберем наибольшее из них.
. Поэтому мы вычислим эти два значения функции и выберем наибольшее из них.
 ,
,  .
.
Согласно теореме Чебышева, на 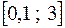 у функции
у функции  должны найтись, по крайней мере, две точки чебышевского альтернанса. Одна из них – это точка
должны найтись, по крайней мере, две точки чебышевского альтернанса. Одна из них – это точка  , в которой функция
, в которой функция  принимает наибольшее значение, а вторая – это точка
принимает наибольшее значение, а вторая – это точка  , в которой функция
, в которой функция  принимает наименьшее значение. В результате мы получим следующие равенства:
принимает наименьшее значение. В результате мы получим следующие равенства:
 ,
,
 ,
,
Вычтем из второго равенства первое и выразим из получившегося равенства  . В результате получим искомый многочлен:
. В результате получим искомый многочлен:
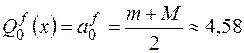 .
.
9. Построить для функции  многочлен наилучшего равномерного приближения первой степени,
многочлен наилучшего равномерного приближения первой степени,  , на
, на  .
.
Решение:
Найдем производные нашей функции и определим характер монотонности функции и направление выпуклости ее графика.  ,
,  . Отсюда следует, что функция
. Отсюда следует, что функция  возрастает, а выпуклость ее графика направлена вниз.
возрастает, а выпуклость ее графика направлена вниз.
Рассмотрим функцию 
 . Согласно теореме Чебышева, на
. Согласно теореме Чебышева, на  найдутся по крайней мере три точки чебышевского альтернанса для этой функции. В рассматриваемом случае две точки чебышевского альтернанса, в которых будет достигаться максимум
найдутся по крайней мере три точки чебышевского альтернанса для этой функции. В рассматриваемом случае две точки чебышевского альтернанса, в которых будет достигаться максимум  , будут, очевидно, совпадать с концами отрезка
, будут, очевидно, совпадать с концами отрезка  . Третья точка, которую мы обозначим
. Третья точка, которую мы обозначим  и в которой будет достигаться минимум
и в которой будет достигаться минимум  , будет находиться внутри отрезка
, будет находиться внутри отрезка  . В первых двух точках значение функции
. В первых двух точках значение функции  будет равно Е, а в третьей – (-Е):
будет равно Е, а в третьей – (-Е):
 ,
,
 ,
,
 .
.
Кроме того, в точке 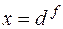 производная функции
производная функции 
 должна обратиться в ноль:
должна обратиться в ноль:
 .
.
Из полученной системы уравнений найдем искомые коэффициенты многочлена наилучшего равномерного приближения. Вычитая из первого уравнения второе, получим:
 .
.
Теперь из последнего уравнения можно будет найти  :
:
 .
.
Складывая первое и третье уравнения, получим:
 .
.
Отсюда находим  .
.
Осталось записать искомый многочлен:  .
.
2.3. Практическая работа № 3. Численное дифференцирование. Метод Рунге-Ромберга
Для студентов специальности «Математическое обеспечение и администрирование информационных систем» отведено 4 часа практических занятий, а для студентов специальности «Программное обеспечение вычислительной техники и автоматизированных систем» - 2 часа.
План занятий:
1. Актуализация определения производной функции одной переменной и дифференциала, его геометрического смысла, понятия бесконечно малой функции  при
при 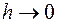 , сравнения бесконечно малых функций при
, сравнения бесконечно малых функций при 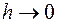 , определения символа «о» - малое и «О» - большое, связь между ними, свойств символа «о» - малое, определения верных цифр в записи приближенного значения и их свойств.
, определения символа «о» - малое и «О» - большое, связь между ними, свойств символа «о» - малое, определения верных цифр в записи приближенного значения и их свойств.
2. Актуализация формулы Тейлора с остаточным членом в форме Лагранжа и Пеано.
3. Повторение полиномиальных формул численного дифференцирования, понятия порядка точности, порядков точности отдельных формул.
4. Повторение оценки погрешности формулы численного дифференцирования при неточно заданных табличных данных, причин начальной стабилизации разрядов в записи приближенных значений производной и последующей разработки.
5. Повторение первой и второй формулы Рунге, асимптотической оценки погрешности, метода повторного счета (правила Рунге).
6. Решение примеров.
7. Консультирование студентов по выполнению домашней работы.
Рассматриваемые примеры:
1. Найти порядок точности и оценку погрешности формулы  при условии, что функция
при условии, что функция  имеет ограниченную производную третьего порядка на
имеет ограниченную производную третьего порядка на 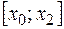 .
.
Решение:
В условиях рассматриваемого примера функцию  можно разложить на указанном промежутке по формуле Тейлора. Запишем это разложение с остаточным членом, записанным в форме Лагранжа и в форме Пеано:
можно разложить на указанном промежутке по формуле Тейлора. Запишем это разложение с остаточным членом, записанным в форме Лагранжа и в форме Пеано:


 при
при  .
.
Здесь точка  лежит между точками x и
лежит между точками x и 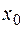 . Используем эти разложения для вычисления
. Используем эти разложения для вычисления  и
и  :
:
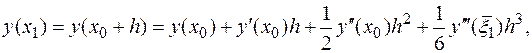


при 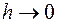 ,
,
 при
при 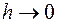 .
.
Здесь точка  лежит между точками
лежит между точками 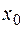 и
и  , а точка
, а точка 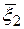 лежит между точками
лежит между точками 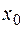 и
и 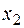 . Рассмотрим разность между точным и приближенным значением производной. Подставим в нее полученные выражения:
. Рассмотрим разность между точным и приближенным значением производной. Подставим в нее полученные выражения:
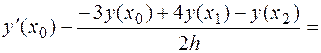

 при
при 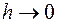 .
.
Таким образом, исследуемая формула численного дифференцирования имеет второй порядок точности. Здесь использовано, что  при
при 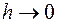 , а также то, что
, а также то, что  при
при 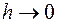 .
.
Подставим в формулу для модуля разности между точным и приближенным значением производной полученные выражения

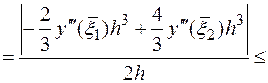

 .
.
Здесь  - это положительная постоянная, такая, что
- это положительная постоянная, такая, что  на
на 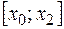 .
.
2. Даны значения функции  в точках
в точках 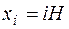 (
( 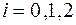 ). На
). На 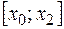 существует ограниченная производная функции второго порядка
существует ограниченная производная функции второго порядка 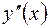 . Для вычисления приближенного значения первой производной функции в точке
. Для вычисления приближенного значения первой производной функции в точке 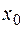 используется формула
используется формула
 .
.
Найти асимптотическую оценку погрешности этого приближенного значения.
Решение:
Наша формула представляет собой приближенную формулу вида  . В самом деле, если положить
. В самом деле, если положить  ,
, 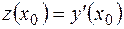 ,
,  , то формула
, то формула  примет вид:
примет вид:  .
.
Формула  , как известно, имеет порядок точности
, как известно, имеет порядок точности 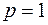 .
.
Выберем  ,
, 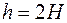 и запишем для рассматриваемой формулы асимптотическую оценку погрешности:
и запишем для рассматриваемой формулы асимптотическую оценку погрешности:


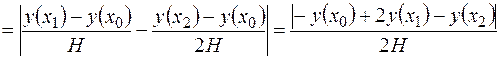 .
.
3. Даны значения функции  в точках
в точках 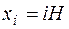 (
( 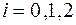 ). На
). На 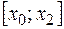 существует ограниченная производная функции второго порядка
существует ограниченная производная функции второго порядка 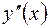 . Для вычисления приближенного значения первой производной функции в точке
. Для вычисления приближенного значения первой производной функции в точке 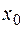 используется формула:
используется формула:
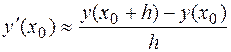 .
.
Вычисление по этой формуле производятся на разреженной сетке с шагом 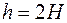 :
:
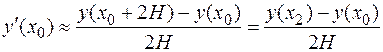 .
.
Используя метод Рунге-Ромберга, уточнить полученное приближенное значение производной.
Решение:
Как мы уже выяснили в предыдущем примере, наша формула представляет собой приближенную формулу вида  , если положить
, если положить 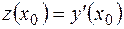 ,
,  , причем формула
, причем формула  , как известно, имеет порядок точности
, как известно, имеет порядок точности 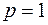 .
.
Выберем  ,
, 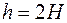 и запишем для рассматриваемого приближенного значения производной
и запишем для рассматриваемого приближенного значения производной  новое уточненное значение
новое уточненное значение  , получаемое по второй формуле Рунге:
, получаемое по второй формуле Рунге:



 .
.
Итак, новое приближенное значение производной  , уточняющее старое приближенное значение
, уточняющее старое приближенное значение  , фактически вычисляется по формуле, порядок точности которой на 1 больше, чем у исходной формулы.
, фактически вычисляется по формуле, порядок точности которой на 1 больше, чем у исходной формулы.
Дата добавления: 2014-11-13; просмотров: 800; Мы поможем в написании вашей работы!; Нарушение авторских прав |