
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средние величины. Понятие о средней величине, её природа и значение
Содержание темы
Понятие о средней величине, её природа и значение. Метод средних как один из важнейших приёмов научного обобщения. Виды средних величин и методы их расчёта. Средняя арифметическая. Средняя гармоническая. Средняя геометрическая. Выбор вида и формы средних.
Понятия, определения, теоретические вопросы
При анализе статистической информации важное место занимают средние статистические показатели. При помощи средней происходит сглаживание различий в величине признака, которые возникают по тем или иным причинам. Средняя величина - один из распространенных способов обобщений количественных показателей.

Рис. 10.1. Классификация средних величин
Рассмотрим признак x (осредняемый признак), по которому необходимо найти среднее значение  . Значения осредняемого признака представлены рядом индивидуальных значений или вариант (х1, х2, х3….хn) (например, вариационным рядом) с частотами индивидуальных значений (f1,f2,f3,…fn) .
. Значения осредняемого признака представлены рядом индивидуальных значений или вариант (х1, х2, х3….хn) (например, вариационным рядом) с частотами индивидуальных значений (f1,f2,f3,…fn) .
Средняя величина является отражением значений изучаемого признака, следовательно, измеряется в той же размерности, что и этот признак.
Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку. Чтобы получить полное и всестороннее представление об изучаемой совокупности по ряду существенных признаков, в целом необходимо располагать системой средних величин, которые могут описать явление с разных сторон.
Существуют различные средние:
* средняя арифметическая;
* средняя геометрическая;
* средняя гармоническая;
Рассмотрим некоторые виды средних, которые наиболее часто используются в статистике.
Средняя арифметическая наиболее распространенный вид средней. Средняя арифметическая обычно используется для характеристики абсолютных величин.
В зависимости от характера исходных данных средняя арифметическая определяется следующим образом.
1. Если каждое значение признака в ряду распределения встречается по одному разу, расчет производится по формуле простой арифметической, которой называется сумма всех значений, деленная на число этих значений.
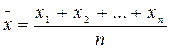 ,или
,или  ,(10.1)
,(10.1)
где x1,x2,…,xn-значения признака (например, цена товара);
n - количество значений.
Например, необходимо вычислить средний возраст сотрудников отдела, если каждому из них 25, 26, 28, 35, 45 лет. Используя формулу (10.1), получим: (25+26+28+35+45)/5= 31,8 года.
2. Если одно и то же значение признака встречается несколько раз, используют формулу средней арифметической взвешенной.Чем чаще встречается определенное значение признака, тем большее влияние на величину средней. Отразить такое влияние представляется возможным посредством следующей формулы:
 , (10.2)
, (10.2)
где xi - значение признака (цена товара),
fi - частота повторения этого признака (вес товара).
Расчет средних величин рассмотрим на основе данных по условному товару (см. табл. 10.1).
Применяя формулу (10.1) для расчета средней цены по данным таблицы, получим
 17,2
17,2
Таблица 10.1.
Экспорт условного товара
| Контракт | Цена товара (долл/кг) | Количество товара (кг) |
Однако, полученное значение средней цены не отражает объема реализации. Поэтому воспользуемся формулой (10.2). Для вышеприведенного примера это значение составит
 23,4 долл/кг.
23,4 долл/кг.
Таким образом, применение формулы расчета средней арифметической взвешенной позволило учесть влияние структуру исходных данных.
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Рассмотрим пример вычисления средней арифметической в дискретном ряду:
| Цена тонны условного товара, долл. Xi | Частота (количество тонн), шт. fi | Произведение вариант на веса (частоты) Xi*fi |
| Итого: |

В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному.
В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.
Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.
Средней гармонической величинойназывают величину, рассчитанную из обратных значений варьирующего признака. Она применяется и как обобщающая характеристика относительных величин.
Также как и средняя арифметическая, средняя гармоническая может быть простой и взвешенной.
Средняя гармоническая простая:
 (10.3)
(10.3)
Средняя гармоническая взвешенная:
 , (10.4)
, (10.4)
где fi - частоты;
Xi - индивидуальные значения.
В приведенном ниже примере необходимо найти, сколько процентов в среднем по стране составил импорт по некоторой товарной группе за 2001 год по сравнению с 2000 годом. Для этой цели можно использовать среднюю гармоническую. В качестве значений признака будут выступать проценты, а в качестве частот – объемы импорта за 2001 год.
Таблица 10.2
| 1 страна | 2 страна | 3 страна | 4 страна | |
| Объем импорта за 2001г, тыс.дол. | ||||
| В % к импорту за 2000г |
 .
.
Средней геометрической принято именовать величину, исчисляемую как корень n–ной степени из произведения n отдельных вариантов признака.
Она также обычно используется для характеристики относительных величин и рассчитывается по формуле:
 , (10.5)
, (10.5)
Пример. Темпы роста в период с 1998-2001 гг. составили соответственно 50%; 40%; 60%; 20%. Определить средний темп роста. Воспользуемся формулой 10.5. Средний темп роста составит
 39%.
39%.
В случаях, когда некоторые либо все варианты (коэффициенты темпов роста, например) относятся к периодам, не одинаковым по продолжительности, средний коэффициент роста исчисляется по формуле средней геометрической взвешенной:
 , (10.6)
, (10.6)
где х - варианты;
fi - веса;
 - сумма весов.
- сумма весов.
Допустим, что коэффициент роста физического объема внешней торговли за периоды:
1994-1998 гг. - 115 %
1998-2001 гг. – 104,7%
2001-2004 гг. прогноз - 101%
Средний темп роста, рассчитанный по формуле 10.6 составит 108%.
При расчете средних величин необходимо помнить о том, что всякие промежуточные вычисления должны приводить как в числителе, так и в знаменателе к имеющим экономический смысл показателям.
Дата добавления: 2014-11-13; просмотров: 915; Мы поможем в написании вашей работы!; Нарушение авторских прав |