
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ряды динамики. Показатели динамики
Содержание темы
Понятие о статистических рядах динамики. Задачи и цель изучения динамики в статистике. Виды рядов динамики (моментные и интервальные). Сопоставимость в рядах динамики - основное условие для эффективного проведения анализа. Статистические показатели динамики (абсолютные приросты, темпы роста, прироста). Определения, методы расчета. Система взаимосвязи показателей динамики цепных и базисных.
Понятия, определения, теоретические вопросы
В статистике внешней торговли для изучения динамики экспорта, импорта, товарооборота в целом применяются относительные величины динамики,которыехарактеризуют изменение изучаемого явления во времени, выявляют направление его развития. Входными данными для такого анализа являются статистические ряды динамики, которые состоят из двух основных элементов: показателя времени (год, месяц, неделя, квартал) и соответствующие показателю времени уровни (стоимостной объем, вес, количество ГТД, удельный вес, коэффициент и т.д.)
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Примером моментного ряда динамики является следующая информация о численности сотрудников таможенного органа в 2001 г.:
| Дата | 1.01 | 1.04 | 1.07 | 1.10 | 1.01 |
| Число работников, чел. |
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть сотрудников, продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет.
В статистике строятся интервальные ряды динамики, которые отображают итоги развития изучаемых явлений за отдельные периоды времени. Примером могут служить данные о товарообороте субъекта РФ по кварталам 1995 года, представленные в таблице:
| 1 кв | 2 кв | 3 кв | 4 кв | |
| Товарооборот (млн.долл) | 305,3 | 401,8 | 397,8 | 406,3 |
В основе расчета показателей динамики лежит сравнение уровней. Если при расчете сравнение происходит с одним и тем же уровнем (базисным), показатели динамики называются базисными. Если последующий уровень ряда сравнивается с предыдущим уровнем, показатели динамики называются цепными.
Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени.
С этой целью для динамических рядов рассчитывают ряд показателей:
К - темпы роста;
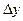 - абсолютные приросты;
- абсолютные приросты;
 - темпы прироста.
- темпы прироста.
Темп роста - относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: 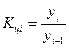 , либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем
, либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем  , выбранным за базу сравнения:
, выбранным за базу сравнения:  . Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.
. Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.
Абсолютный прирост - разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базисными, в зависимости от способа выбора базы для сравнения:
цепной абсолютный прирост -  ;
;
базисный абсолютный прирост -  .
.
Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста.
Темп прироста - относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.
Базисные темпы прироста: 
 .
.
Цепные темпы прироста: 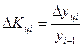 .
.
 и
и  - абсолютный базисный или цепной прирост;
- абсолютный базисный или цепной прирост;
 - уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;
- уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;
 - уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
- уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
Существует связь между темпами роста и прироста:
 К = К - 1 или
К = К - 1 или  К = К - 100 % (если темпы роста определены в процентах).
К = К - 100 % (если темпы роста определены в процентах).
Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый - абсолютное значение одного процента прироста:  .
.
По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин - средний абсолютный прирост, средний темп роста, средний темп прироста.
Средний абсолютный прирост может быть получен по одной из формул:
 или
или 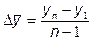 ,
,
где n - число уровней ряда динамики;
 - первый уровень ряда динамики;
- первый уровень ряда динамики;
 - последний уровень ряда динамики;
- последний уровень ряда динамики;
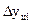 - цепные абсолютные приросты.
- цепные абсолютные приросты.
Средний темп роста можно определить, пользуясь формулами:

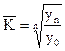

где n - число рассчитанных цепных или базисных темпов роста;
 - уровень ряда, принятый за базу для сравнения;
- уровень ряда, принятый за базу для сравнения;
 - последний уровень ряда;
- последний уровень ряда;
 - цепные темпы роста (в коэффициентах);
- цепные темпы роста (в коэффициентах);
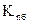 - последний базисный темп роста.
- последний базисный темп роста.
Между темпами прироста  и темпами роста К существует соотношение
и темпами роста К существует соотношение  =К–1. Средний темп прироста вычислим с помощью данного соотношения:
=К–1. Средний темп прироста вычислим с помощью данного соотношения: 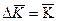 -1
-1
Дата добавления: 2014-11-13; просмотров: 340; Мы поможем в написании вашей работы!; Нарушение авторских прав |