
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка надежности результатов корреляционного анализа
Анализируемые ряды динамики являются почти всегда выборками из более длинных рядов. Поэтому необходима всесторонняя проверка надежности результатов корреляционного и регрессионного анализа. Основой проверки является теория выборочного наблюдения.
Значение коэффициента корреляции r является случайной величиной, которая зависит от объема выборки. При увеличении объема числовой информации распределение выборочного коэффициента корреляции приближается к нормальному.
В практике анализа используемые ряды динамики представляют собой малые выборки. Следует отметить, что оценки, полученные на основе коротких рядов, не имеют особенного значения в качестве характеристик фактических параметров. Одни оценки могут быть лучше других, но ни одна из них не является совершенно надежной. Сказанное особенно относится к выборкам из совокупностей, не подчиненных нормальному распределению.
Несмотря на это, необходима оценка результатов анализа даже при малых выборках. При этом конечной целью является не оценивание фактических параметров (коэффициентов корреляции и регрессии), а проверка, варьируются ли найденные параметры в некотором интервале за счет влияния случайных факторов или нет.
Например, если надо проверить надежность коэффициента корреляции, то это не означает, что мы должны определить его величину в генеральной совокупности. Наша цель имеет более общий характер: можем ли мы получить такой коэффициент корреляции на основе выборки из совокупности, где корреляции нет, т. е. проверка надежности корреляции в совокупности.
Полученные результаты и выводы являются правильными только при нормально распределенных совокупностях. Но практические результаты показывают, что допустимо некоторое удаление от нормального распределения. Однако, если есть основание предполагать, что распределение существенно отличается от нормального, то результаты корреляционного и регрессионного анализа не противостоят критике.
Выше изложенное, конечно, не означает, что при распределениях, отличных от нормального, связи между явлениями нет. Дело в том, что методика исследования связей в таких совокупностях связана с существенными математическими трудностями.
И еще одно обстоятельство. При малых выборках надежность оценивается с более низкой вероятностью, чем в больших выборках. Обычно ограничиваются 95%-ной вероятностью оценки (вероятность ошибки — уровень значимости— 5%).
Критерий Стьюдента. Рассмотрим применение t-критерия для проверки надежности результатов корреляционного анализа. Пусть извлечена выборка объема N, и вычислен выборочный коэффициент корреляции r. Для проверки существенности линейной корреляции определяется величина  . Поверка нулевой гипотезы (отсутствие линейной корреляции) состоит в сравнении значения tr с табличным значением критической точки распределения Стьюдента
. Поверка нулевой гипотезы (отсутствие линейной корреляции) состоит в сравнении значения tr с табличным значением критической точки распределения Стьюдента 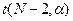 при заданном уровне значимости
при заданном уровне значимости  и числе степеней свободы N-2.
и числе степеней свободы N-2.
Если tr< 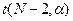 , то гипотеза об отсутствии линейной связи принимается;
, то гипотеза об отсутствии линейной связи принимается;
Если tr 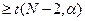 , то гипотеза об отсутствии линейной связи отвергается.
, то гипотеза об отсутствии линейной связи отвергается.
Пример:проверить с надежностью 95% гипотезу о наличии линейной связи между стоимостными показателями X и Y.
| Стоимость,X | ||||||||||
| Стоимость,Y |
Построим вспомогательную таблицу
| Стоимость, X | Стоимость, Y | (X-Xср)2 | (Y-Yср)2 | XY | |
| Средние | 25,8 | 156,4 | 539,8 |
Найдем коэффициент линейной корреляции r=0,28 и вычислим критерий Стьюдента 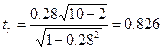 . По таблице критических точек распределения Стьюдента находим
. По таблице критических точек распределения Стьюдента находим  . Поскольку
. Поскольку 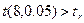 , то с надежностью 95% можно утверждать, что линейной связи между показателями X и Y не наблюдается.
, то с надежностью 95% можно утверждать, что линейной связи между показателями X и Y не наблюдается.
Дата добавления: 2014-11-13; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |