
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корреляция и регрессия
Содержание темы
Корреляционная связь и зависимость. Простая корреляция и регрессия. Индекс и коэффициент линейной корреляции.
Общественные явления находятся в постоянном изменении и развитии. Изменения одного явления часто вызывают изменения другого или нескольких других явлений, следовательно, явления в некоторой степени связаны между собой. При этом в статистической литературе нередко говорят о «корреляционной зависимости» между явлениями. Термины «связь» и «зависимость» имеют различный смысл и поэтому необходимо различать содержание «корреляционной связи» и «корреляционной зависимости». Слово «зависимость» приводит к мысли о причинности. Если нам заранее известно, что изменение одного явления является причиной изменения другого, то использование термина «корреляционная зависимость» является обоснованным. Но если это неизвестно, необходимо употреблять термин «корреляционная связь», чтобы избежать ложной интерпретации результатов анализа
Корреляционной называют такую связь, при которой одному значению одного явления соответствует определенное множество значений другого. Например, фиксированной цене на нефть соответствует определенный диапазон цен на бензин. Целью анализа корреляции является исследование тесноты связи между явлениями.
По своей форме связи могут быть весьма простыми или очень сложными. Общественные явления, в том числе и экономические, имеют, как правило, сложные связи.
Корреляционный анализ является одним, но не единственным методом выявления связи между явлениями. Но только корреляционный анализ дает простую оценку тесноты связи. Это обстоятельство обусловливает широкое применение корреляционного анализа в экономических исследованиях.
Установив наличие корреляционной связи, применяют регрессионный анализ. Регрессионный анализ является методом статистического анализа связей между явлениями, целью которого является анализ формы связи. Результаты регрессионного анализа – это функциональная связь между явлениями.
Эффективность методики корреляционного и регрессионного анализа зависит от решения многих проблем. Корреляционному и регрессионному анализу предшествовать всесторонний основательный теоретический анализ возможности существования связи между исследуемыми явлениями. Только при возможности реальной связи можно пользоваться методикой корреляционного и регрессионного анализа и получать результаты, имеющие реальный смысл.
Необходимо выявить все явления, оказывающие влияние на исследуемый объект, и провести их подробный анализ. Также надо выявить логическую структуру связей между исследуемыми явлениями. Очень важным при анализе является выбор связи: хотя разработаны некоторые методы оценки правильности выбора формы связи, все-таки нужен профессиональный экономический анализ. Количественные результаты анализа влияния факторов зависят от формы связи, и таким образом, конечные результаты анализа находятся в прямой связи от формы связи. С другой стороны, сложные формы связи значительно затрудняют работу исследователя и опять могут привести к ложным результатам.
Подчеркиваем еще раз, что механическое использование методики корреляционного и регрессионного анализ всегда приводит к ложным результатам.
Простая корреляция и регрессия.Простой корреляцией принято называть корреляцию между двумя переменными. Целью анализа является оценка наличия и тесноты связи между двумя явлениями. При определении формы связи между двумя экономическими явлениями x и y (например, рядами динамики) наиболее часто пользуются следующими функциями:
прямая линия у = а0 +a1 х
парабола у = a0+a1x +a2x2
гипербола у = а0 + a1/x
показательная функция y=a0a1x
Пусть по данным, полученным в результате n наблюдений выбрана форма связи и методом наименьших квадратов подобраны коэффициенты: y=f(x). Обобщенной оценкой тесноты связи между двумя переменными является индекс корреляции.
 , где
, где  ;
;  .
.
Абсолютное значение индекса корреляции находится в пределах:
 .
.
Если R = 1, имеем дело с функциональной связью, если R = 0, исследуемые явления между собой не связаны. Выбранная функциональная связь между явлениями тем лучше, чем ближе значение индекса корреляции единице. Часто применяется следующая классификация при оценке тесноты связи:
0. . . 0,2 — слабая связь; 0,2 ... 0,4 — слабее средней тесноты; 0,4 ... 0,6 — средняя теснота; 0,6 ... 0,8 — теснее средней; 0,8 ... 1 — сильная связь.
Следует отметить, что такая классификация является условной. В экономике она может быть принятой для характеристики корреляции в генеральных совокупностях.
Индекс корреляции пригоден для оценки тесноты связи при любой форме парной связи. Для анализа наличия линейной зависимости между явлениями можно пользоваться коэффициентом корреляции r:
 , где
, где 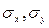 - среднее квадратическое отклонение, x и y, а
- среднее квадратическое отклонение, x и y, а  -средние значения показателей x, y и их произведений.
-средние значения показателей x, y и их произведений.
Коэффициент корреляции r принимает значения в интервале [-1;1]. Положительное значение коэффициента корреляции указывает на прямую связь, а отрицательное значение - на обратную связь между явлениями. Чем ближе к 0 коэффициент корреляции, тем слабее линейная связь между явлениями. Близость | r | к единице говорит о сильной линейной связи. Для классификации силы линейной связи обычно применяется соответствующий аналог для индекса корреляции. Однако, следует помнить, что отсутствие линейной связи не означает отсутствие любой связи между изучаемыми явлением. Например, коэффициент линейной корреляции при квадратичной зависимости между двумя явлениями может равняться нулю.
Пример.Определить наличие линейной корреляции и охарактеризовать связь между ценой товара и объемами поставок.
| Цена X | ||||||||||
| Объем Y |
Построим вспомогательную таблицу.
| Цена, X | Объем, Y | (X-Xср)2 | (Y-Yср)2 | XY | |
| средние | 25,2 |
Согласно формуле исчисления коэффициента линейной корреляции, 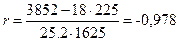 . Найденный коэффициент говорит о сильной обратной линейной связи.
. Найденный коэффициент говорит о сильной обратной линейной связи.
Дата добавления: 2014-11-13; просмотров: 359; Мы поможем в написании вашей работы!; Нарушение авторских прав |