
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дисперсионный анализ
В более сложных случаях исследуют воздействие нескольких факторов на нескольких постоянных или случайных уровнях и выясняют влияние отдельных уровней и их комбинаций (многофакторный анализ).
Мы ограничимся простейшим случаем однофакторного анализа, когда на X воздействует только один фактор, который имеет р постоянных уровней F1, F2,..., Fp.
Пусть на количественный нормально распределенный признак X воздействует фактор F, который имеет р постоянных уровней. Будем предполагать, что число наблюдений на каждом уровне одинаково и равно q. Пусть наблюдалось n — pq значений Хij признака, где i — номер испытания (i — 1, 2, ..., q), j—номер уровня (j=1, 2, ...,р). Рассмотрим факторную группировку.
| Номер наблюдения | Уровни фактора F , | |||
| F1 | F2 | … | Fp | |
| X11 | X12 | … | X1p | |
| X21 | X22 | … | X2p | |
| … | … | … | … | … |
| q | Xq1 | Xq2 | … | Xqp |
Введем, факторную и остаточную дисперсии.
Факторная дисперсия характеризует рассеяние между группами.
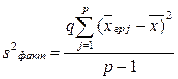
Остаточная дисперсия характеризует рассеяние «внутри групп».
 , где
, где  .
.
Убедимся, что sфакт характеризует воздействие фактора F. Допустим, что фактор оказывает существенное влияние на X. Тогда группа наблюдаемых значений признака на одном определенном уровне, вообще говоря, отличается от групп наблюдений на других уровнях. Следовательно, различаются и групповые средние, причем они тем больше рассеяны вокруг общей средней, чем большим окажется воздействие фактора. Отсюда следует, что для оценки воздействия фактора целесообразно составить сумму квадратов отклонений групповых средних от общей средней (отклонение возводят в квадрат, чтобы исключить погашение положительных и отрицательных отклонений). Итак, sфакт характеризует воздействие фактора.
Убедимся, что sОСТ отражает влияние случайных причин. Казалось бы, наблюдения одной группы не должны различаться. Однако, поскольку на X, кроме фактора F, воздействуют и случайные причины наблюдения одной и той же группы, вообще говоря, различны и значит, рассеяны вокруг своей групповой средней. Отсюда следует, что для оценки влияния случайных причин целесообразно составить сумму квадратов отклонений наблюдаемых значений каждой группы от своей групповой средней. Итак, sОСТ характеризует воздействие случайных причин.
Пусть нулевая гипотеза о равенстве групповых средних ложна. В этом случае с возрастанием расхождения между групповыми средними увеличивается факторная дисперсия, а вместе с ней и отношение 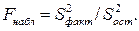 В итоге Fнабл окажется больше Fкр(
В итоге Fнабл окажется больше Fкр( 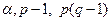 ) и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.
) и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.
Таким образом, если гипотеза о равенстве групповых средних ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий. Для того чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию Фишера F нулевую гипотезу о равенстве факторной и остаточной дисперсий. В этом и состоит метод дисперсионного анализа.
После того, как установлено то, что фактор существенно влияет на X, а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то дополнительно производят попарное сравнение средних. Как правило, приходится иметь дело с малыми выборками. В этом случае используют
Дата добавления: 2014-11-13; просмотров: 674; Мы поможем в написании вашей работы!; Нарушение авторских прав |