Сравнение нескольких дисперсий

Пусть признаки Х₁, Х₂, ..., Х_р распределены нормально. Требуется при заданном уровне значимости по выборочным исправленным дисперсиям 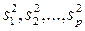проверить нулевую гипотезу Н₀:D(Х₁) = D(Х₂) = ... =D(X_p) о равенстве всех дисперсий. Другими словами, требуется установить, значимо или незначимо различаются выборочные дисперсии. Пусть объем каждой выборки равен n.

В качестве критерия проверки нулевой гипотезы примем критерий Кочрена G - отношение максимальной исправленной дисперсии к сумме всех исправленных дисперсий

.

Если , то нет оснований отвергнуть гипотезу о равенстве дисперсий, где - критическая точка распределения Кочрена (приложение 4), - уровень значимости, n-1 - число степеней свободы, p - количество выборок. Если , то гипотезу отвергают.

Пример. Установить с уровнем значимости 5% факт влияния ставки таможенной пошлины на объем экспорта продукции в стоимостном выражении (тыс. долл.).

Решение. Вычислим групповые средние 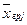и исправленные дисперсии S²_j.

	Значение ставки пошлины
Показатель	5%	10%	15%
Средние,	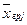29,00	22,57	14,57
Исправленные дисперсии, S2j	9,33	6,29	7,62

Чтобы воспользоваться дисперсионным анализом необходимо проверить гипотезу о равенстве дисперсий. Воспользуемся критерием Кочрена. Критическая точка распределения Кочрена =0,6771, S²_max=9.33, а критерий Кочрена G=0.4. Поскольку , гипотеза о равенстве дисперсий принимается.

Вычислим факторную и остаточную дисперсии , , 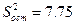а также критерий Фишера . По таблице для уровня значимости 5% находим критическую точку Фишера F_кр( )=3.55. Поскольку F_набл >F_кр( ), гипотеза о влиянии фактора принимается c уровнем значимости 5%.

Вывод Изменение таможенной пошлины влияет на стоимостные объемы экспорта данной продукции.