Коротко о главном

Уровни ряда динамики формируются под вниманием 3-х групп факторов:

1. Постоянно действующих факторов, определяющих основное направление, т.е. тенденцию развития изучаемого явления. Основная тенденция развития называется трендом.

2. Периодически действующих факторов, т.е. направленных колебаний по неделям месяца, месяцам года и т.д.

3. Разовых кратковременных факторов, которые действуют в разных, иногда в противоположных направлениях и оказывают случайное влияние на уровни данного ряда динамики.

Таким образом, ряд динамики y_t может быть представлен в виде суммы трех компонент:

Ø тренда (детерминированной непериодической функции f_t)

Ø циклической (детерминированной периодической функции g_t)

Ø белого шума (случайной функции e_t)

y_t=f_t+g_t+e_t

Основной задачей статистического изучения динамики является выявление тенденции.

Основными методами выявления тенденции рядов динамики являются:

- метод укрупнения интервалов

- метод скользящей средней

- метод аналитического выравнивания

1. Сущность метода укрупнения интервалов заключается в следующем:

Исходный ряд динамики преобразуется и заменяется другими состоящими из других уровней, относящихся к укрупненным периодам или моментам времени.

Например: помесячный ряд динамики прибыли малого предприятия за 1997-2000 годы можно представить по кварталам. При этом уровни ряда за укрупненные периоды или моменты времени могут представлять собой либо суммарные, либо средние показатели. Однако в любом случае рассчитанные таким образом уровни ряда более отчетливо выявляют тенденции, поскольку сезонные и случайные колебания при суммировании или определении средних взаимопогашаются и уравновешиваются.

2. Метод скользящей средней, как и предыдущий предполагает преобразование исходного ряда динамики. Для выявления тенденции формируются интервал, состоящий из одинакового числа уровней. При этом каждый последующий интервал получается путем смещения на 1 уровень от начального. По образованным таким образом интервалам определяются в начале сумма, а затем средние. Технически удобнее определять скользящие средние для нечетного интервала. В этом случае рассчитанная средняя величина будет относиться к конкретному уровню ряда динамики, т.е. к середине интервала скольжения.

При определении скользящей средней по четному интервалу, расчетное значение средней величины относится к промежутку между двумя уровнями, и таким образом теряют экономический смысл. Это делает необходимыми дополнительные расчеты, связанные с центрированием по формуле арифметической простой из двух соседних не центрированных средних.

3. Метод аналитического выравниваниязаключается в выборе адекватной математической функции, которая наилучшим образом отражает тенденцию развития ряда динамики. Аналитически тренд представляется как функция f(t), зависящая от времени. Реальные данные y_t называют эмпирическими уровнями ряда динамики. Точки, принадлежащие линии тренда, это значения f(t) для соответствующих значений t. Их называют расчетными значениями, или теоретическими уровнями ряда динамики. При построении функции тренда необходимо решить две задачи: определить класс функции для описания зависимости и оценить параметры этой функции.

Выбор класса математической функции для описания линии тренда предварительно осуществляется на основе логики связи и визуального анализа ряда динамики. В качестве модели тренда можно использовать любую подходящую функцию, однако чаще всего используют:

прямую f(t) = a0+ a1t

параболу второго порядка f(t) = a0+ a1t +a2t2

экспоненту: f(t) = a 0a1t

Линейная функция или прямая используется для моделирования равномерного развития. Положительные значения a1свидетельствуют о росте, отрицательные - о спаде.

Парабола служит для описания квадратичной зависимости от времени. Параметр а₂ – постоянное ускорение. Если а₂ положительное, то движение равноускоренное, а если а₂ отрицательное – равнозамедленное.

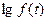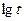Экспонента отражает пропорциональную связь между и . Параметр a₁в уравнении экспоненты показывает, во сколько раз изменится f(t) за единицу времени. Положительные значения a₁ свидетельствуют о прямой связи, отрицательные – об обратной.

Если более сложная зависимость от времени не может быть достаточно корректно описана перечисленными функциями, то часто этого удается достичь посредством замены переменных. Следует помнить, что необоснованное усложнение модели приводит к менее надежным оценкам, получаемым по ней.

Согласно критерию наименьших квадратов параметры модели подбираются таким образом, чтобы сумма квадратов отклонений фактических значений от расчетных была минимальной.

Q = S (y_t – f(t))2= min.

 

Если в качестве линии тренда выбрана прямая f(t) = a0+ a1t, то критерий наименьших квадратов можно записать:

 

Q = S (y_t – a0- a1t)2= min.

Чтобы из этого условия определить числовые значения a0и a1, следует взять первые частные производные от Q по a0и a1и приравнять их нулю, в результате получим систему нормальных уравнений:

S у_t = a0n + a1S t

S ty_t = a0 S t + a1S t2

Центрируя время так, чтобы 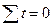, получим формулы для параметров a0и a1:

,

.

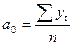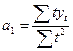Аналогично получаются системы уравнений для параболы и экспоненты.

Основной характеристикой точности модели является ошибка аппроксимации

.

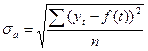Чем меньше ошибка 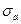, тем лучше модель.

Прогнозирование осуществляется экстраполированием (продолжением по времени) функции тренда f(t).

На практике прогнозирование осуществляется с помощью интервальных оценок. Границы доверительного интервала рассчитываются по формуле:

,

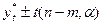
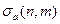где 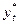- прогнозное значение, равное f(t),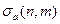 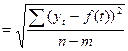- ошибка аппроксимации, скорректированная по числу степеней свободы n-m (n – число уровней ряда динамики, m – число параметров модели), а 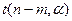- критическая точка распределения Стьюдента с числом степеней свободы - n-m и уровнем значимости (см. Приложение 2 ).

Пример.Построить линейную модель товарооборота фирмы и дать прогноз на декабрь.

Месяц	Товарооборот, тыс.долл.
январь	10,4
февраль	10,9
март	10,8
апрель	11,2
май	11,6
июнь	11,5
июль	11,8
август	12,1
сентябрь	12,6
октябрь	12,4
ноябрь	12,5

 

Проведем центрирование времени. В результате, июню будет соответствовать t=0, маю - t=-1, июлю - t=1 и т.д. Составим вспомогательную таблицу (все вычисления удобно проводить в электронной таблице Excel).

 

	t	yt	t2	t yt	f(t)=0.22t+11.6	(yt-f(t))2
	-5	10,4		-52	10,5	0,0174
	-4	10,9		-43,6	10,7	0,0228
	-3	10,8		-32,4	11,0	0,0277
	-2	11,2		-22,4	11,2	0,0003
	-1	11,6		-11,6	11,4	0,0396
		11,5			11,6	0,0140
		11,8		11,8	11,8	0,0013
		12,1		24,2	12,1	0,0022
		12,6		37,8	12,3	0,1089
		12,4		49,6	12,5	0,0076
		12,5		62,5	12,7	0,0418
сумма		127,8		23,9		0,2835
	a0=	11,6	a1=	0,22		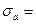0,1606
		t(9,0.05)=	2,26		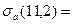	0,177497

 

Прогноз на декабрь: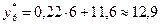

Доверительный интервал для прогноза с уровнем значимости 5%:

.

Таким образом, с вероятностью 95% можно утверждать, что в декабре товарооборот фирмы приблизительно составит от 12,52 до 13,32 тыс. долларов.