
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурные средние величины
Содержание темы
Понятие моды и медианы. Особенности и применение структурных средних.
Понятия, определения, теоретические вопросы
В ряде случаев необходимо знать значение признака, которое чаще всего встречается. Например, для того чтобы определить какая цена является наиболее предпочтительной при экспорте/импорте того или иного товара участниками ВЭД, используется показатель моды. Мода - статистический показатель, который характеризует чаще всего встречающееся значение признака и исчисляется для интервальных рядов распределения по формуле:


 (11.1)
(11.1)
где  - нижняя граница модального интервала
- нижняя граница модального интервала
 - длина интервала
- длина интервала

 - частота, соответствующая модальному интервалу (т.е. интервалу, имеющему наибольшую частоту)
- частота, соответствующая модальному интервалу (т.е. интервалу, имеющему наибольшую частоту)

 - частота интервала, предшествующего модальному интервалу
- частота интервала, предшествующего модальному интервалу

 - частота интервала, следующего за модальным интервалом.
- частота интервала, следующего за модальным интервалом.
Данная формула основана на том, что расстояния от нижней границы модального интервала до моды и от моды до верхней границы модального интервала прямо пропорциональны разностям между численностью модального интервала и прилегающих к нему. При этом модальным интервалом является тот, который имеет наибольшую частоту (частость).
Пример: По данным таблицы вычислим моду
Таблица 11.1
| Стаж | Число таможенников |
| до 2 | |
| 4-6 | |
| 6-8 | |
| 8-10 | |
| 10-12 | |
| 12-14 | |
| свыше 14 |
Наибольшая частота соответствует интервалу сотрудников таможенных органов со стажем от 8-10 лет, который и является модальным. Моду определим по формуле: 8+2*(35-20)/((35-20)+(35+12))=8+2*0,24=8,5 года. Таким образом, в данной совокупности наиболее часто встречается стаж таможенников 8,5 лет.
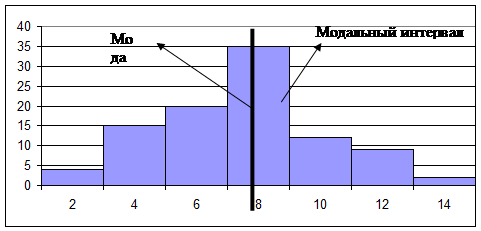 |
Рис. 11.1. Распределение таможенников в зависимости от стажа работы.
Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой. Например, имеется совокупность (дискретный вариационный ряд), содержащая сведения о среднедневном оформлении таможенниками грузовых таможенных деклараций (ГТД).
Таблица 11.2.
| Количество ГТД, оформленных в день (шт.) | Число таможенников, частота (чел.) |
Наибольшей частотой является число 20. Этой частоте соответствует модальное значение признака, количество оформленных в день ГТД. Мода свидетельствует, что в данном примере чаще всего встречаются работники, оформляющие 24 ГТД в день.
Медиана (  ) – это значение показателя, приходящееся на середину ранжированного ряда наблюдений.
) – это значение показателя, приходящееся на середину ранжированного ряда наблюдений.
Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).
Например, стаж пяти таможенников составил 2, 4, 7, 8, 10 лет. В таком упорядоченном ряду медиана - 7 лет. По обе стороны от нее находится одинаковое число таможенников.
Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Пусть теперь будет не пять таможенников, а шесть, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 6 и 7. Средняя арифметическая из этих значений и будет медианой ряда: Ме = (6 + 7) / 2 = 6,5 лет.
В случае непрерывного вариационного ряда для вычисления медианы нам понадобится понятие накопленная частость.
Накопленная частость  –это сумма частостей, соответствующих интервалам 1,..,j. Интервал называется медианным, если накопленная частость этого интервала больше 50%, а предыдущего интервала – меньше. Медиана вычисляется по формуле
–это сумма частостей, соответствующих интервалам 1,..,j. Интервал называется медианным, если накопленная частость этого интервала больше 50%, а предыдущего интервала – меньше. Медиана вычисляется по формуле
 , (11.2)
, (11.2)
где  - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
 - длина интервала;
- длина интервала;
 - накопленная частность предшествующего интервала;
- накопленная частность предшествующего интервала;
 - частость медианного интервала.
- частость медианного интервала.
Пример. Определить моду и медиану по заданной выборке цен:
| x | 10,1-10,3 | 10,3-10,5 | 10,5-10,7 | 10,7-10,9 | 10,9-11,1 |
| f |
Модальным будет интервал 10,5-10,7, так как ему соответствует наибольшая частота 10. Получаем: xj=10,5,  =0,2,
=0,2,  ,
, 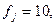
 ;
;
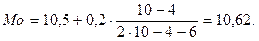
Построим дополнительно таблицу для частостей и накопленных частостей.
| x | 10,1-10,3 | 10,3-10,5 | 10,5-10,7 | 10,7-10,9 | 10,9-11,1 |

| 2/23 | 4/23 | 10/23 | 6/23 | 1/23 |

| 2/23 | 6/23 | 16/23 | 22/23 |
Медианным будет также интервал 10,5-10,7. Получаем: xj=10,5,  =0,2,
=0,2,  ,
, 

Дата добавления: 2014-11-13; просмотров: 342; Мы поможем в написании вашей работы!; Нарушение авторских прав |