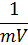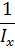КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выделение уравнений продольного движения из полной системы уравнений продольного движения самолета.
Наличие у ЛА плоскости материальной симметрии позволяет разделить его пространственное движение на продольное и боковое. К продольному движению относится движение ЛА в вертикальной плоскости при отсутствии крена и скольжения, при нейтральном положении руля и элеронов. При этом происходят два поступательных и одно вращательное движение. Поступательное движение осуществляются вдоль вектора скорости и по нормали, вращательное – вокруг оси Z. Продольное движение характеризуется углом атаки α, углом наклона траектории θ, углом тангажа, скоростью полета, высотой полета, а также положением руля высоты и величиной и направлением в вертикальной плоскости тяги ДУ.
Система уравнений продольного движения самолета.
Замкнутая система, описывающая продольное движение самолета может быть выделена из полной системы уравнений, при условии, что параметры бокового движения, а также углы отклонения органов управления креном и рысканьем равны 0.



 (6.1)
(6.1)
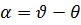
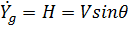
Соотношение α = ν – θ оплучено из первого геометрического уравнения после его преобразования.
Последнее уравнение системы 6.1 не влияет на остальные и может быть решено отдельно. 6.1 – нелинейная система, т.к. содержит в себе произведения переменных и тригонометрических функций, выражения для аэродинамических усилий.
Для получения упрощенной линейной модели продольного движения самолета, необходимо ввести определенные допущения и провести процедуру линеаризации. С целью обоснования дополнительных допущений, нам необходимо рассмотреть динамику продольного движения самолета при ступенчатом отклонении руля высоты.
Реакция самолета на ступенчатое отклонение руля высоты. Разделение продольного движения на долго- и кратковременное.
При ступенчатом отклонении δв возникает момент Мz(δв), который вращает относительно оси Z со скоростью ωz. При этом происходит изменение угла тангажа и атаки. При увеличении угла атаки возникает приращение подъемной силы и соответствующий этому момент продольной статической устойчивости Мz(Δα),который противодейсвует моменту Мz(δв). По истечению вращения, на определенном угле атаки он его компенсирует.
Изменение угла атаки после уравновешивания моментов Мz(Δα) и Мz(δв) останавливается, но, т.к. самолет обладает определенными инерциальными свойствами, т.е. обладает моментом инерции Iz относительно оси ОZ, то установление угла атаки носит колебательный характер.
Угловые колебания самолета вокруг оси ОZ будут демпфировать ся с помощью собственного момента аэродинамического демпфирования Мz(ωz). Приращение подъемной силы начинает изменять направление вектора скорости. Изменяется также угол наклона траектории θ.Это в свою очередь влияет на угол атаки.Исходя из сбалансированности моментных нагрузок синхронно с изменением угла наклона траектории продолжает изменяться угол тангажа. При этом угол атаки – постоянный. Угловые движения на малом интервале происходят с высокой частотой, т.е. имеют короткий период и называются краткопериодическими.
После того, как затухнут кратковременные колебания, становится заметным изменение скорости полета. В основном за счет составляющей Gsinθ. Изменение скорости ΔV влияет на приращение подъемной силы, и как следствие, на угол наклона траектории. Последнее изменяет скорость полета. При этом возникают угасающие колебания вектора скорости по величине и направлению.
Указанные движения характеризуются низкой частотой, угасают медленно, поэтому их называют долгопериодическими.
При рассмотрении динамики продольного движения нами не была учтена дополнительная подъемная сила, создаваемая отклонением руля высоты. Данное усилие направлено на уменьшение полной подъемной силы, поэтому ддля тяжелых самолетов наблюдается явление просадки – качественное отклонение угла наклона траектории с одновременным увеличением угла тангажа. Это происходит пока приращение подъемной силы не скомпенсирует составляющую подъемной силы за счет отклонения руля высоты.
На практике, долгопериодические колебания не возникают, т.к. своевременно гасятся пилотом, или автоматическими органами управления.
Передаточные функции и структурные схемы матмодели продольного движения.
Передаточной функцией называется изображение выходной величены, по изображению входной при нулевых начальных условиях.
Особенностью передаточных функций самолета, как объекта управления является то, что отношение выходной величины, по сравнению со входной берется с отрицательным знаком. Это связано с тем, что в аэродинамике принято в качестве положенительного отклонения органов управления считать отклонения, которые создают отрицательные приращения параметров движения самолета.

В операторной форме записи имеет вид:

 (6.10)
(6.10)

Системе 6.10, которая описывает кратковременное движение самолета соответствуют решения:
 (6.11)
(6.11)
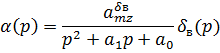
 (6.12)
(6.12)

Таким образом, можем записать передаточные функции, которые связывают угол атаки и угловую скорость по тангажу от отклонения руля высоты
 (6.13)
(6.13)

Для того, чтобы передаточные функции имели стандартный вид, введем следующие обозначения:
 ,
,  ,
,  ,
,  ,
, 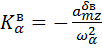 ,
,

Учитывая эти соотношения перепишем 6.13:
 (6.14)
(6.14)
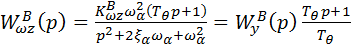 (6.15)
(6.15)


Таким образом, передаточные функции по углу наклона траектории и по углу тангажа, в зависимости от отклонения руля высоты будут иметь следующий вид:
 (6.16)
(6.16)
 (6.17)
(6.17)
Одним из важнейших параметров, которые характеризуют продольное движение самолета является нормальная перегрузка. Перегрузка бывает: Нормальной (по оси ОУ), продольная (по оси ОХ) и боковая (по оси OZ). Вычисляется как сумма сил, действующих на самолет в определенном направлении, деленная на силу тяжести. Проекции на оси позволяют вычислить величину и соотношение ее с g.
 -нормальная перегрузка,
-нормальная перегрузка,
Из первого уравнения сил системы 6.3 получим:

Используя выражения для перегрузки перепишем:


Для условий горизонтального полета (  :
:

 (6.18)
(6.18)

Запишем структурную схему, которая соответствует передаточной функции:




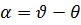

 | |||
|









|
 ωz ν ν
ωz ν ν
 |

|



 α
α

|
 | ||||||
|
| |||||





|
 θ θ
θ θ
 |
Боковая сила Za(δн) создает момент крена Мх(δн). Соотношение моментов Мх(δн) и Мх(β) характеризует прямую и обратную реакцию самолета на отклонение руля направления. В случае, если Мх(δн)по модулю больше, чем Мх(β), самолет будет наклоняться в противоположную сторону разворота.
Принимая во внимание вышесказанное можем построить структурную схему для анализа бокового движения ЛА при отклонении руля направления.






|
|
|
|

|
 ωy ψ ψ
ωy ψ ψ
 |  |  |  | ||||||||||
 |  | ||||||||||||
 | |||||||||||||



|
- 




 Ψ1
Ψ1
 | ||||||
|
| |||||



|



 Fz
Fz  Ψ1
Ψ1
 | |||||
| |||||
| |||||





|

 | |||
 | |||


|
 |
γ
В режиме так называемого плоского разворота моменты крена компенсируются пилотом, либо соответствующей системой управления. Следует отметить, что при малом боковом движении самолет кренится, вместе с этим происходит наклон подъемной силы, что вызывает боковую проекцию Yasinγ, которая начинает развивать большое боковое движение: самолет начинает скользить на наклоненное полукрыло, при этом увеличиваются соответствующие аэродинамические силы и моменты, и значит роль начинают играть так называемые "спиральные моменты": Му(ωх) и Му(ωz). Большое боковое движение целесообразно рассматривать при уже наклоненном самолете, или на примере динамики самолета при отклонении элеронов.
Реакция самолета на отклонение элеронов.
При отклонении элеронов возникает момент Мх(δэ). Самолет начинает вращаться вокруг связанной оси ОХ, при этом появляется угол крена γ. Демпфирующий момент Мх(ωх) противодействует вращению самолета. При наклоне самолета вследствии изменения угла крена возникает боковая сила Zg(Уа), которая является результирующей от силы веса и подъемной силы Уа. Эта сила "разворачивает" вектор скорости, при этом начинает меняться путевой угол Ψ1, что приводит к возникновению угла скольжения β и соответствующей силы Za(β), а также момента путевой статической устойчивости Му(β), который начинает разворачивать продольную ось самолета с угловой скоростью ωу. Вследствие такого движения начинает меняться угол рысканья ψ. Боковая сила Za(β) направлена в противоположную сторону по отношению к силе Zg(Уа) поэтому она в некоторой степени уменьшает скорость изменения путевого угла Ψ1.
Сила Za(β) также является причиной момента поперечной статической устойчивости. Мх(β), который в свою очередь старается вывести самолет из крена, а угловая скорость ωу и соответствующий ей спиральный аэродинамический момент Мх(ωу) стараются увеличить угол крена. Если Мх(ωу) больше Мх(β) – возникает ак называемая "спиральная неустойчивость", при которой угол крена после возвращения элеронов в нейтральное положение продолжает увеличиваться, что приводит к развороту самолета с возрастающей угловой скоростью.
Такой разворот называется координированным разворотом, при этом угол крена задается пилотом, либо с помощью системы автоматического управления. При этом в процессе разворота компенсируются возмущающие моменты по крену Мхβ и Мхωу, руль направления при этом компенсирует скольжение, то есть β, Za(β), Му(β) = 0, при этом момент Му(β), который разворачивал продольную ось самолета, замещается моментом от руля направления Му(δн), а боковая сила Za(β), которая препятствовала изменению путевого угла замещается силой Za(δн). В случае координированного разворота скорость (маневренность) увеличивается, при єтом продольная ось самолета совпадает с вектором воздушной скорости и разворачивается синхронно с изменение угла Ψ1.

γ
 | ||||||||
|
|
| ||||||
δэ 









|

|
 ωx γ Za Fy
ωx γ Za Fy
 | |||
 | |||



|
|

 |  | ||||||||
|
|
|


|
 ωy ψ Ψ1
ωy ψ Ψ1
 |  |  | |||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 β
β
| |||
 | |||

 ψ
ψ
 |
Дата добавления: 2014-12-03; просмотров: 475; Мы поможем в написании вашей работы!; Нарушение авторских прав |