
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Универсальный пример шкалирования
| 1 нравится | не нравится | |||||||||
| сильно | слабо | слабо | сильно | |||||||
| очень сильно | сильно | слабо | очень слабо | очень слабо | слабо | сильно | очень сильно | |||
| 4 8 | -2 | -4 | -6 | -8 | ||||||
| 5 8 |
Таким образом, здесь наблюдается переход от шкалы наименований (строка 1, где имеются только 2 класса), к шкале порядковой (строки 2 и 3, где имеется порядок, но еще не существует чисел), а затем к интервальной (строка 4, где ноль относительный) и шкале отношений (строка 5, где ноль абсолютный).
Таблица 2.3.
Другой пример шкалирования
| Количественные значения и интенсивность относительной важности | Содержательное определение предпочтения |
| Равная важность | |
| Умеренное (легкое) превосходство | |
| Заметно существенное превосходство | |
| Значительное превосходство | |
| Очень сильное превосходство |
Движение в шкалировании идет от номинальной (или шкалы наименований) к порядковой шкале, а затем к интервальной шкале или шкале отношений. При этом «сила» измерения возрастает, а самая «сильная» шкала - шкала отношений.
Измерение можно представить как иерархию моделей. Наблюдатель проводит измерение по следующим шагам: определение задачи, наблюдение, гипотеза, эксперимент, проведенные измерения, принятие или непринятие гипотезы.
4. Измерение свойств и признаков результативности формальной организации.Измеряемые признаки результативности функционирующего предприятия:
· основные, сопряженные и побочные, желательные и не желательные;
· действенность, производительность, экономичность, прибыльность, качество, качество трудовой жизни.
Основные результаты - это те, ради которых создается формальная организация и осуществляется работа. Они выражаются в форме целей и задач.
Сопряженные и побочные - это те результаты, которые сопутствуют основному, но могут быть как желательными (прибавляются к основному), так и не желательными (вычитаются из основного).
Пример измерения показателей результативности предприятия по Д.С.Синку приводится в таблице 2.4.
Таблица 2.4.
Свойства результативности и ее измеряемые признаки
| Критерии измерения | Отношение измеряемых признаков |
| 1.Действенность или эффективность | Индексы, показывающие степень достижения цели (норм) в одном периоде по сравнению с другим периодом |
| 2. Экономичность | Ресурсы, подлежащие потреблению/Ресурсы, фактически потребленные |
| 3. Качество* | Произведен и доставлен ли продукт так, как было задумано и требовалось; удовлетворен ли покупатель товаром; будет ли товар выполнять то, для чего он предназначен |
| 4. Прибыльность | Чистый доход (после вычета налогов)/0бъем продаж; Чистый доход/Совокупные активы; Чистый доход/ Собственный капитал |
| 5.Производитель-ность | Надлежащая продукция/Фактически потребленные ресурсы |
| 6. Качество трудовой жизни | Могут измеряться как индексы, интегрирующие ответы персонала на вопросы о состоянии дел по перечисленным аспектам |
| 7. Внедрение новшеств | В строгом смысле количественное измерение пока не применяется |
5. Проблемы управления, возникающие в связи с измерением. Трудности измерения: проблема языка как средства коммуникации, детализации исходных данных, стандартизации условий измерения, точности измерения. Содержание затруднений приводятся в таблице 2.5.
Таблица 2.5.
Содержание затруднений, имеющихся в измерении.
| Трудности измерения | Содержание затруднений |
| Языка | проблема включает в себя не только нахождение количественных результатов, но и способ их передачи или как следует выразить результаты измерения, чтобы донести их до других; количественные результаты мы можем получить с помощью кем то разработанной шкалы или разработать шкалу самостоятельно, но в любом случае самостоятельно существует проблема содержательной интерпретации количественного значения измеренного признака; таким образом, в начале, строя шкалу, мы идем от номеров к числам, а затем, интерпретируя полученные в результате измерения числа, мы идем в обратном направлении - от чисел к номерам. |
| Детализации | какие исходные данные следует использовать применительно к стоящей задаче: содержательные (общие) или количественные (частные) |
| Стандартизации | нахождение условий, при которых гарантируется правильность измерения |
| Точности | как оценить отклонение, которое существует всегда, чтобы контролировать желаемые результаты |
Иллюстрации проблем измерения сделаны ниже на рис.2.2,2.3. и 2.4. для случаев существования неясности и неопределенности.
Между неопределенностью и неясностью существует различие, которое должно учитываться в измерении для ситуаций, а) когда хорошо описанное событие может произойти, а может и не произойти, что означает наличие неопределенности; б) когда существует неточное описание и плохое определение события, что означает наличие неясности. Поэтому статистика и теория вероятностей являются языком неопределенности, а теория размытых множеств - языком неясности.
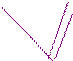
Размытые множества: идея экспертных оценок, при которых вес важности назначается в некоторых границах, например при важности в 6 баллов максимальное значение может быть 8, а минимальное - 5. В результате мы получаем три кривых или три точки, а выбор эксперта зависит от степени его склонности к риску

 мах риск
мах риск
 |
 медиана
медиана
 мин риск
мин риск
 |
Рис. 2.2 Графическое выражение функции принадлежности теории размытых множеств.
Симплекс метод: оптимум находится в многограннике АВСDE
 | |||
 | |||
 A
A


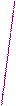




 E
E
 |

 B
B
 |

 C
C
D
 |
Рис. 2.3. Графическое выражение оптимума при 5 переменных.
Метод наименьших квадратов: кривая отражает наименьшую степень среднеарифметических или среднеквадратических отклонений каждого значения исследуемого множества от ближайшей точке на кривой.
 |
Рис. 2.4. Графическое выражение метода наименьших квадратов.
Задание для самостоятельной работы.
1. Постройте интервальную шкалу и шкалу отношений, используя для этого подготовленный ниже рисунок.
2. Перечислите шаги построения шкалы наименований, а также постройте ее одному и двум признакам.
Вопросы для самопроверки (впишите пропущенные слова)
| 1. Измерение предшествует ____________________. |
| 2.Измерение представляет собой выражение свойств с помощью _________ и/или _____________. |
| 3.Существует ________шкалы измерения. |
| 4.Самая «слабая» шкала называется шкала ________________. |
| 5. Самая «сильная» шкала называется шкала ________________. |
| 6.Для того, чтобы отличить номер от числа используется правило _______________. |
| 7. В чем состоит значение чисел как инструмента измерения: |
Дата добавления: 2014-12-03; просмотров: 264; Мы поможем в написании вашей работы!; Нарушение авторских прав |