Момент силы.

Одна и та же сила может сообщать вращающемуся телу разные угловые ускорения в зависимости от её направления и точки приложения. Для характеристики вращающего действия силы вводят понятие момента силы.

Различают момент силы относительно неподвижной точки и относительно неподвижной оси. Моментом силы относительно точки О (полюса) называется векторная величина, равная векторному произведению радиус-вектора проведенного из точки О в точку приложения силы, на вектор силы:

Поясняющий это определение рис. 3 выполнен в предположении, что точка О и вектор лежат в плоскости чертежа, тогда вектор так же располагается в этой плоскости, а вектор ^ к ней и направлен от нас (как векторное произведение 2-х векторов; по правилу правого буравчика).

Модуль момента силы численно равен произведению силы на плечо:

,

где - плечо силы относительно точки О, a - угол между направлениями и , .

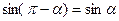Плечо - кратчайшее расстояние от центра вращения до линии действия силы.

Вектор момента силы сонаправлен с поступательным движением правого буравчика, если его рукоятку вращать по направлению вращающего действия силы. Момент силы - аксиальный (свободный) вектор, он направлен вдоль оси вращения, не связан с определенной линией действия, его можно переносить в

пространстве параллельно самому себе.

Моментом силы относительно неподвижной оси Z называется проекция вектора на эту ось (проходящую через точку О).

Если на тело действуют несколько сил, то результирующий момент сил относительно неподвижной оси Z равен алгебраической сумме моментов относительно этой оси всех сил, действующих на тело.

Если сила, приложенная к телу, не лежит в плоскости вращения, её можно разложить на 2 компоненты: лежащую в плоскости вращения и ^ к ней F_n. Как видно из рисунка 4, F_n вращения не создает, а приводит только к деформации тела; вращение тела обусловлено только составляющей F_t .

Вращающееся тело можно представить как совокупность материальных точек.

Выберем произвольно некоторую точку с массой m_i , на которую действует сила , сообщая точке ускорение (рис. 5). Поскольку вращение создает только тангенциальная составляющая, для упрощения вывода направлена перпендикулярно оси вращения.

В этом случае

.

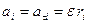Согласно второму закону Ньютона: . Умножим обе части равенства на r_i;

,

,

где - момент силы, действующей на материальную точку,

- момент инерции материальной точки.

Следовательно, .

Для всего тела: ,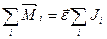

,

, (1)

т.е. угловое ускорение тела прямо пропорционально моменту действующих на него внешних сил и обратно пропорционально его моменту инерции. Уравнение

(1) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси, или второй закон Ньютона для вращательного движения.