
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 27. Доказать рефлексивность, транзитивность и монотонность отношения ⊨.
27. Доказать рефлексивность, транзитивность и монотонность отношения ⊨.
28. Свойство монотонности отношения логического следования говорит, что если к логически корректному умозаключению добавить еще какие-то допущения, оно останется логически правильным. А если к логически неправильному умозаключения добавить посылки, оно (а) останется неправильным, (б) станет правильным или (в) может стать правильным? Ответ поясните.
29. А если из правильного убрать посылки?
30. А из неправильного?
31. Определите, являются ли следующие умозаключения правильными, опираясь только на знание правильных (modus ponens, modus tollens) и неправильных условно-категорических умозаключений, а также ряда законов логики (де Морган и коммутативности и др.) и свойства транзитивности и монотонности отношения логического следования.
1) Если ты умнее Аристотеля, то я китайский император. Но ты не умнее. Значит, я не император.
2) Если ты умнее Аристотеля, то я китайский император. Но я не император. Значит, ты не умнее.
3) Только если сегодня суббота, у меня есть шанс выспаться. Шанс есть. Значит, суббота.
4) Если сегодня суббота, у меня есть шанс выспаться. Шанс есть. Значит, суббота.
5) Если ты умнее Аристотеля, то я китайский император. Но я не император. Да и ты тоже. Значит, ты не умнее.
6) Если завтра экзамен по логике или математике, то сегодня меня терзают смутные предчувствия. Предчувствий нет, даже смутных. Значит, завтра нет ни логики, ни математики.
7) Если завтра экзамен по логике или математике, то сегодня меня терзают смутные предчувствия. Предчувствий нет, даже смутных. Значит, завтра нет логики или математики.
8) Если завтра экзамен по логике или математике, то сегодня меня терзают смутные предчувствия. Предчувствий нет, даже смутных. Значит, завтра логики нет.
32. Наличие противоречия (т.е. утверждения вида «А и не-А») в теории, основанной на классической логике, имеет для нее катастрофические последствия. Какие? Казалось бы, ну получил ты, что какое-то утверждение, и его отрицание верны, ну, выпил триста капель валерьянки, успокоился, живешь и работаешь дальше, изучаешь свою теорию. Почему не так? (И дело не в валерьянке и не в количестве капель.)
33. Для следующих схем рассуждения определите, являются ли они логически корректными, не строя таблицы истинности (в некоторых случаях предполагается, что студенты знают ряд законов КЛВ).
(a) p&Øp, qÉØr ⊨ Ør
(b) p& q1&q4&Øp&s, qÉØr ⊨ ØrÉq
(c) p&q1&q4&s, q1 º p, q ⊨ (ØrÚØq1ÚsÚrÚp)&(pÚØqÚØsÚØpÚØq4)
(d) p&q1&q4&s, rÚq1ÚsÚs1Úp ⊨ p4Úq4Ús4Úq4
(e) T⊨Ø(p & q) º (Øр & Øq)
(f) ^⊨Ø(p & q) º (Øр & Øq)
(g) p⊨Ø(p & q) º (Øр Ú Øq)
(h) T⊨ (р É q) º (q É p)
Ответы
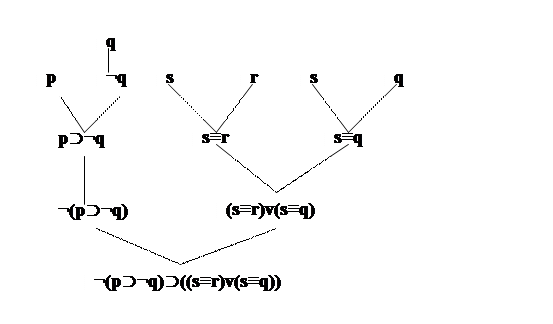
Гл.3 Упр.2 (с)
Подформулы:
q , p, s, r
q
p⊃q
(p⊃q)
s≡r
s≡q
(s≡r)v(s≡q)
(p⊃q)⊃((s≡r)v(s≡q))
(то есть все формулы, расположенные в узлах дерева)
Главный знак – вторая импликация:
((p⊃q)⊃((s≡r)v(s≡q)))
(вторая импликация – последний при построении данной формулы знак).
Нагруженное дерево формулы:
Гл.3 Упр.6
1. q É р
2. р É q
3. р º q
4. p1 & р2 & р3 & r & Øq
5. p É (r Ú q)
6. 1-й вариант: (r Ú q)É р
2-й вариант: Øp É Ø(r Ú q)
7. (p1& р2 & р3 & r) É q
8. 1-й вариант: (p1Úр2Ú р3Ú r) É q
2-й вариант: Øq É Ø (p1Úр2Ú р3Ú r) )
9. p º (r Ú Øq)
10. 1-й вариант: q É ((s1 & s2 & s3 & Øs4 ) É (p1 & р2 & р3 & r))
2-й вариант: (q & s1 & s2 & s3 & Øs4 ) É (p1 & р2 & р3 & r)
11. 1-й вариант: (q1 Ú q2) É (Ø (s1 Ú s2) É (p1 & р2 & р3 & r))
2-й вариант: ((q1 Ú q2) & Ø (s1 Ú s2)) É (p1 & р2 & р3 & r)
12. (s1 Ú s2 ) º (р & Øs)
13. 1-й вариант: Ø р É Ø (p1 & р2)
2-й вариант: (p1 & р2) É р
14. Øр É (p1 & р2)
15. Øр º (p1 & р2)
Гл.3 Упр.9
a.И ты прав, и я, а преподаватель не прав.
| простые предложения, входящие в состав предложения | символизация |
| Я прав. | p |
| Ты прав. | q |
| Преподаватель прав. | r |
Структура: q&p&Ør
b. Я пью крепкий кофе, если и только если хочу спать или у меня много работы.
| простые предложения, входящие в состав предложения | символизация |
| Я пью крепкий кофе. | p |
| Я хочу спать. | q |
| У меня много работы. | r |
Структура: р º (q Ú r)
c.Я займусь изучением логики, если скоро зачет по этому предмету и преподаватель не ставит "автоматы".
| простые предложения, входящие в состав предложения | символизация |
| Я займусь изучением логики. | p |
| У меня скоро зачет по логике. | q |
| Преподаватель логики ставит автоматы. | r |
Структура: (q & Ør) É р
d. Я займусь изучением логики, только если скоро зачет по этому предмету и преподаватель не ставит "автоматы".
Символизация, та же, что в предыдущем примере.
Структура:
1-й вариант: Ø(q & Ør) É Øр
2-й вариант: р É (q & Ør)
e.Я займусь изучением логики, если скоро зачет по этому предмету или преподаватель не ставит "автоматы", разве что буду уверен, что сумею списать.
| простые предложения, входящие в состав предложения | символизация |
| Я займусь изучением логики. | p |
| У меня скоро зачет по логике. | q |
| Преподаватель логики ставит автоматы. | r |
| Я буду уверен, что сумею списать. | s |
Структура
1-й вариант: (q Ú Ør) É (ØsÉр)
2-й вариант: ((q Ú Ør) & Øs)Éр
f. Если ты знаешь английский, французский, испанский и немецкий, в Европе ты не пропадешь, если имеешь пару тысяч долларов, евро или фунтов стерлингов.
| простые предложения, входящие в состав предложения | символизация |
| Ты знаешь английский. | p |
| Ты знаешь французский. | q |
| Ты знаешь испанский. | r |
| Ты знаешь немецкий. | s |
| В Европе ты пропадешь. | p1 |
| У тебя есть пару тысяч долларов. | q2 |
| У тебя есть пару тысяч евро. | r2 |
| У тебя есть пару тысяч фунтов. | s2 |
Структура
1-й вариант: (р&q&r&s) É((q2 Ú r2 Ú s2 ) É p1)
2-й вариант: (р & q & r & s & (q2 Ú r2 Ú s2 )) É p1
g.Если ты работаешь пять дней в неделю, то я всего лишь два.
| простые предложения, входящие в состав предложения | символизация |
| Ты работаешь пять дней в неделю. | p |
| Я работаю два дня в неделю. | q |
Структура: р & q. (Вариант р É q неверен.)
h. Я выучу английский, китайский или японский, только если буду усердно заниматься, у меня будет достаточно свободного времени и, кроме того, я смогу съездить в страну изучаемого языка.
| простые предложения, входящие в состав предложения | символизация |
| Я выучу английский. | p |
| Я выучу китайский. | q |
| Я выучу японский. | r |
| Я буду усердно заниматься. | s |
| У меня будет достаточно свободного времени. | p1 |
| Я смогу съездить в страну изучаемого языка. | q1 |
Структура:
1-й вариант: Ø (s & p1 & q1) É Ø (р Ú q Ú r)
2-й вариант: (р Ú q Ú r) É (s & p1 & q1)
i. Если у меня будет много свободного времени, я выучу английский и японский, а если не будет, тогда только английский.
| простые предложения, входящие в состав предложения | символизация |
| У меня будет много свободного времени. | p |
| Я выучу английский. | q |
| Я выучу японский. | r |
Структура: (р É (q&r)) & (Øр É (q&Ør))
Гл.3 Упр.11(а)
Москва – столица России - истина,
Рим – столица Греции – ложь.
Предложения соединены союзом "а", с логической точки зрения – конъюнкцией. Если с помощью конъюнкции соединяются истинное и ложное предложение, результирующее предложение – по определению конъюнкции – будет ложным.
Ответ: логическое значение данного высказывания – ложь.
Гл.3 Упр. 12(а) Будем вычислять значение формулы в следующем порядке:
1 2 6 3 5 4
(Øр É q) & (Øq É Ør)
ϕ1 (Øр)= л; (при этой оценке р полагаем истинным, тогда его отрицание будет ложным – по определению отрицания)
ϕ1 (Øр É q)= и;
ϕ1 (Øq)= л;
ϕ1 (Ør) =и;
ϕ1 (Øq É Ør) = и;
ϕ1 ((Øр É q) & (Øq É Ør))=и.
Дата добавления: 2014-11-13; просмотров: 291; Мы поможем в написании вашей работы!; Нарушение авторских прав |