Лекция 8. ГЛОБАЛЬНЫЕ КОМПЬЮТЕРНЫЕ СЕТИ

Законы Ома дают возможность рассчитать практически любую сложную цепь, однако непосредственный расчет разветвленных цепей сложен и гораздо проще осуществляется с помощью 2-х правил Кирхгофа.

Представим разветвленную цепь постоянного тока, обозначим все ее элементы и произвольным образом зададим предполагаемые направления токов. Первое правило Кирхгофа относится к узлам цепи.

Узлом разветвленной цепи называется точка, в которой соединяюся более двух проводников. Участок цепи от узла до следующего узла называется ветвью.

Поскольку в случае постоянного тока нигде в цепи не должны накапливаться заряды (иначе токи не оставались бы постоянными), сумма токов, текущих к узлу, должна быть равна сумме токов, текущих от узла (в соответствии с законом сохранения заряда).

Ток, текущий к узлу, договорились считать условно положительным, от узла - отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю, .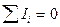

Можно записать N - 1 независимых уравнений для N узлов цепи.

Второе правило относится к любому замкнутому контуру, выделенному в разветвленной цепи.

Выберем произвольное направление обхода контура. Все токи, направление которых совпадает с направлением обхода, считаются положительными, направленные противоположно - отрицательными. Э.д.с. считается положительной, если при выбранном направлении обхода внутри источника тока переход совершается от «минуса» к «плюсу», т.е. в сторону повышения потенциала.

Второе правило Кирхгофа: в любом замкнутом контуре, выделенном в разветвленной цепи алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме э.д.с, .

При расчете цепи с использованием правил Кирхгофа необходимо помнить следующее.

1. Число уравнений равно числу искомых величин.

2. Для N узлов записывается N-1 уравнений, а остальные - в соответствии со вторым правилом.

3. Токи, текущие к узлу, положительны, от узла - отрицательны.

4. Целесообразно направление обхода выбирать так, чтобы большинство токов были положительны, т.е. совпадали по направлению с обходом контура.

5. В одной ветви от узла до узла течет один ток.

6. Обход лучше начинать с узла и вернуться к этому же узлу.

7. Контуры выбираются таким образом, чтобы каждый новый контур содержал хотя бы один участок цепи, не входивший в уже рассмотренные контуры.

Лекция 8. ГЛОБАЛЬНЫЕ КОМПЬЮТЕРНЫЕ СЕТИ

Потребность в обмене информацией и современные технические достижения сделали глобальные компьютерные сети неотъемлемой частью осуществления программ сотрудничества между странами. Создано множество компьютер­ных сетей для научных и образовательных целей, для бизнеса, финансово-экономической деятельности, реализации совместных научно-технических про­ектов и многих других применений. Сетью, способной объединить множество сетей и позволяющей войти в мировое сообщество, является Internet. Internet предоставляет пользователю практи­чески неограниченные информационные ресурсы. Чтобы получить доступ к этим ресурсам, необходимо воспользоваться соответствующим прикладным про­граммным обеспечением. Дружественный графический интерфейс этого про­граммного обеспечения сделал услуги Internet доступными каждому. Многие из таких программ работают в привычной для пользователя среде Windows. Программы с графическим интерфейсом обладают важной особенностью: они скрывают от пользователя всю системную архитектуру и позволяют работать одинаково с информацией, сохраняемой на компьютерах любой платформы.