Понятие об энтропии. Второе начало термодинамики.

1. Рассмотрим обратимый процесс.

Из уравнений для цикла Карно следует, что

(1)

Уравнение (1) означает, что количество теплоты, полученное или отданное при обратимом процессе, пропорционально температуре.

Отношение называется приведенным количеством теплоты.

Из (1) следует, что для обратимого цикла Карно

Условились считать положительным, когда система поглощает тепло, и отрицательным - когда выделяет.

Q₂ - количество теплоты, отдаваемое рабочим телом холодильнику, поэтому оно отрицательное. Следовательно, можно записать

,

т.е. для обратимого цикла алгебраическая сумма приведенных количеств теплоты равна нулю.

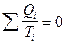
или в дифференциальной форме:

(2)

Интеграл берется по замкнутому контуру, т.к. рассматривался цикл - круговой процесс.

- приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса.

Из равенства нулю интеграла (2), взятого по замкнутому контуру следует, что подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние.

Таким образом,

- элементарная энтропия, .

Функция состояния, дифференциалом которой является ,называетсяэнтропией.

Изменение энтропии при переходе системы из состояния 1 в состояние 2

.

При обратимом процессе

. (3)

2. При необратимом процессе DS>.

, .

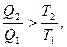
(4)

Соотношения (3) и (4) можно представить в виде неравенства Клаузиуса :

DS 0,

т.е. энтропия замкнутой системы может либо возрастать (при необратимых процессах), либо оставаться постоянной (при обратимых процессах). Это означает, что изменение энтропии в замкнутой системе есть мера необратимости совершающихся в ней процессов.

Само слово "энтропия" происходит от греческого глагола "энтропив" - преобразовать, превратить, и было предложено одним из основоположников термодинамики Клаузиусом.

Наиболее чёткий смысл энтропии дал Больцман в 1877г., введя в теорию теплоты статистические представления. Он приписал каждому состоянию системы "термодинамическую вероятность" W.

Термодинамическая вероятность W равна количеству способов, которыми можно реализовать данное состояние. W тем больше, чем более беспорядочным или неопределённым является состояние.

Действительно, если " порядок " можно осуществить сравнительно небольшим число способов, то " беспорядок" - очень большим.

Чем больше число элементов в системе, тем большее значение принимает W.

Больцманом было показано, что логарифм W связан с S следующим образом:

,

где k - постоянная Больцмана.

При таком подходе возрастание энтропии означает, что система, предоставленная самой себе, переходит из одного состояния в другое, W которого больше. С точки зрения статистики энтропия является мерой беспорядка в системе.

Т.о. энтропия замкнутой системы не может уменьшаться, DS

Это утверждение носит название второго закона термодинамики.

Его можно сформулировать по-другому, но смысл от этого не изменится.

Некоторые формулировки:

невозможен самопроизвольный процесс перехода тепла от тела, менее нагретого, к телу, более нагретому;

невозможен процесс, единственным результатом которого было бы полное превращение тепла в работу;

невозможно создать вечный двигатель второго рода.

В состоянии равновесия энтропия системы достигает максимального значения.

Стремления любой системы к самопроизвольному увеличению энтропии, приводящему к выравниванию во всех частях системы температуры, было использовано идеалистами для создания теории " тепловой смерти" Вселенной. По этой теории энтропия Вселенной в конце концов должна достигнуть максимума, температура во всей Вселенной должна выровняться и всякое движение материи - прекратиться. Однако это не так. Законы статистической физики справедливы для огромного, но не бесконечного числа тел. В бесконечной Вселенной возможны процессы менее вероятные, протекающие с уменьшением энтропии, вследствие чего " тепловая смерть "Вселенной не наступает никогда, движение материи вечно и неуничтожимо.

III начало термодинамики (принцип Нернста ): при любом изотермическом процессе при Т=0, DS=, S=S₀=const

или ( в формулировке Планка ): при Т=0 энтропия системы равна 0.

Из 3^го начала следует, что невозможен такой процесс, в результате которого тело могло быть охлаждено до Т=0.