Оптимальные демодуляторы двумерных полосовых сигналов

В случае двумерных сигналов ФМ-M (M ³ 4), АФМ-M, КАМ-M канальные символы описываются

, (10.1)

где а_сі и а_sі – пары коэффициенты, которые отображают n = log₂M передаваемых бит согласно модуляционному коду.

Канальные символы состоят из косинусных и синусных импульсов. Их необходимо разделить. Это осуществляется с помощью двух синхронных детекторов, которые отличаются опорными колебаниями – если опорное колебание cos2pf₀t, то детектор не реагирует на синусную составляющую входного сигнала, если опорное колебание sin 2pf₀t, то детектор не реагирует на косинусную составляющую входного сигнала. Поэтому с помощью двух детекторов осуществляется разделение косинусного и синусного импульсов и последующая их раздельная обработка в двух подканалах демодулятора (рис. 10.1): согласованная фильтрация и дискретизация. Оценки коэффициентов поступают на схему решения.

Как и в случае одномерных сигналов, правило вынесения решений формулируется на основе разбивки пространства сигналов на М непересекающихся областей s_i, i = 0, …, М – 1; каждая область s_i – это совокупность точек, которые ближе к сигналу s_i(t), чем к другим сигналам. Отличие заключается в том, что пространство сигналов двумерное. Если точка ( ) попала в область сигнала s_i, то выносится решение о том, что передавался сигнал s_i. Схема решения выдает решение битами согласно модуляционному коду.

На рис. 10.2 показанная разбивка пространств канальных символов на области сигналов. Границы областей показаны жирными линиями. В случае сигнала ФМ-4 области сигналов – 4 квадранта; в случае сигнала ФМ-8 области сигналов – 8 секторов; в случае сигнала КАМ-16 области сигналов образованы вертикальными и горизонтальными прямыми. Благодаря простоте разбивки пространства двумерных сигналов КАМ-М на области сигналов они получили самое широкое распространение среди сигналов АФМ-М.

К двумерным сигналам относятся также сигналы ЧМ-2. Канальные символы описываются

, (10.2)

где Df – разнос частот.

Если разнос частот удовлетворяет условию Df = k/(2Т), где k = 1, 2, …, то сигналы ортогональные, и они могут быть разделены синхронными детекторами (аналогично разделению косинусного и синусного импульсов). Схема оптимального демодулятора сигнала ЧМ-2 подобна схеме, приведенной на рис. 10.1, но отличается опорными колебаниями в синхронных детекторах (рис. 10.3).

На рис. 10.4 показанная разбивка пространства канальных символов ЧМ-2 на области сигналов. Граница областей показана жирной линией. Из этого рисунку видно, что для вынесения решения о переданном сигнале достаточно сравнить оценки амплитуд сигналов s₀(t) и s₁(t): если > , то выносится решение 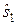и наоборот.

Контрольные вопросы

1. Объясните назначение отдельных блоков оптимального демодулятора двумерных сигналов КАМ-M и ФМ-М.

2. Сформулируйте правило вынесения решения на основе разбивки пространства канальных символов на М областей.