
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вероятность ошибки при оптимальной демодуляции двумерных сигналов цифровой модуляции
При анализе помехоустойчивости двумерных сигналов может возникнуть одна из двух ситуаций.
1. Линия, которая соединяет сигналы si и sj, входящие в формулу (11.9), совпадает с одной из осей координат пространства сигналов. В этом случае вероятность ошибки в двоичной системе, использующей сигналы si и sj, определяется формулой (11.6), как и в случае одномерных сигналов.
2. Линия, которая соединяет сигналы si и sj, входящие в формулу (11.9), не совпадает ни с одной из осей координат пространства сигналов (рис. 12.1). На этом рисунке показаны шумовые компоненты оценок: 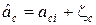 и
и  , где zс и zs – гауссовские независимые величины с нулевым средним и СКО
, где zс и zs – гауссовские независимые величины с нулевым средним и СКО  – формула (5.14). На основе рис. 12.1 условие возникновения ошибки – вынесение решения о передаче
– формула (5.14). На основе рис. 12.1 условие возникновения ошибки – вынесение решения о передаче 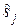 , если было передано si
, если было передано si
 Pош(si, sj) = Р {h > d/2}, (12.1)
Pош(si, sj) = Р {h > d/2}, (12.1)
где h = zс cos a +zs cos (90°– a) гауссовская случайная величина. Ее дисперсия
 . (12.2)
. (12.2)
Таким образом, и в случае ситуации 2 вероятность ошибки (12.1) определяется формулой (11.6), как и в случае одномерных сигналов.
Упражнение 12.1. Найдем вероятность ошибки для многопозиционного двумерного сигнала ФМ-4 (рис. 12.2): координаты канальных символов ±а, а расстояния между ближайшими символами d = 2a. Энергии канальных символов одинаковые  . Энергия сигнала на бит
. Энергия сигнала на бит

 . (12.3)
. (12.3)
Из рис. 12.2 видно, что достаточно учесть переходы лишь в два ближайших канальных символа, поэтому, учитывая формулу (11.6)
 . (12.4)
. (12.4)
Учитывая формулы (11.10) и (12.4), получим выражение для вероятности ошибки двоичного символа при ФМ-4
 . (12.5)
. (12.5)
 Упражнение 12.2. Найдем вероятность ошибки для многопозиционного сигнала ФМ-М. Точки сигнального созвездия находятся на окружности радиуса а с угловым шагом 2p/М. Ясно, что достаточно учесть переходы лишь в два ближайших канальных символа. На рис.12.3 приведен фрагмент сигнального созвездия сигнала ФМ-М. Выразим расстояние между ближайшими точками через радиус окружности. Поскольку d/2 = a×sin(p/M), то d = 2a sin(p/M). Энергии канальных символов одинаковые: Е = а2. Энергия сигнала на бит определяется
Упражнение 12.2. Найдем вероятность ошибки для многопозиционного сигнала ФМ-М. Точки сигнального созвездия находятся на окружности радиуса а с угловым шагом 2p/М. Ясно, что достаточно учесть переходы лишь в два ближайших канальных символа. На рис.12.3 приведен фрагмент сигнального созвездия сигнала ФМ-М. Выразим расстояние между ближайшими точками через радиус окружности. Поскольку d/2 = a×sin(p/M), то d = 2a sin(p/M). Энергии канальных символов одинаковые: Е = а2. Энергия сигнала на бит определяется  и расстояние
и расстояние  .
.
Используя формулы (11.10) и (12.4), получим выражение для вероятности ошибки двоичного символа при ФМ-М для М ³ 4
 . (12.5)
. (12.5)
 Упражнение 12.3. Найдем вероятность ошибки для многопозиционных двумерных сигналов КАМ-16 (рис. 12.4). Возьмем одну из четырех точек, которые размещены возле начала координат. Для любой из них видно, что достаточно учесть переходы лишь в четыре ближайших канальных символа, поэтому, учитывая формулу (11.6)
Упражнение 12.3. Найдем вероятность ошибки для многопозиционных двумерных сигналов КАМ-16 (рис. 12.4). Возьмем одну из четырех точек, которые размещены возле начала координат. Для любой из них видно, что достаточно учесть переходы лишь в четыре ближайших канальных символа, поэтому, учитывая формулу (11.6)
 . (12.6)
. (12.6)
Найдем среднюю энергию канального символа
Еср = (4×2а2 + 8×10а2 + 4×18а2)/16 = 10а2. (12.7)
Энергия сигнала на бит определяется 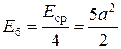 и расстояние
и расстояние  .
.
Используя формулы (11.10) и (12.6), получим выражение для вероятности ошибки двоичного символа при КАМ-16
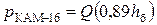 . (12.8)
. (12.8)
Можно получить общую формулу вероятности ошибки бита для сигналов КАМ-М (М ³ 16) при условии, что log2M является четным числом
 . (12.9)
. (12.9)
 Упражнение 12.4. Найдем вероятность ошибки для двоичного сигнала ЧМ-2 (рис. 12.5): координаты канальных символов равны а, а расстояние между символами d =
Упражнение 12.4. Найдем вероятность ошибки для двоичного сигнала ЧМ-2 (рис. 12.5): координаты канальных символов равны а, а расстояние между символами d =  a. Энергии канальных символов одинаковые
a. Энергии канальных символов одинаковые  .
.
По формуле (11.6) получим
 . (12.10)
. (12.10)

Полученные в разд. 11 и 12 формулы позволяют определить вероятности ошибки бита р при заданном отношении сигнал/шум  или необходимое отношение сигнал/шум при заданной вероятности ошибки бита. Анализ помехоустойчивости удобно проводить, используя графики зависимости р = f (
или необходимое отношение сигнал/шум при заданной вероятности ошибки бита. Анализ помехоустойчивости удобно проводить, используя графики зависимости р = f (  ) (рис. 12.6). При построении графика отношение сигнал/шум принято выражать в децибелах и использовать для него линейный масштаб. Для вероятности ошибки используют логарифмический масштаб.
) (рис. 12.6). При построении графика отношение сигнал/шум принято выражать в децибелах и использовать для него линейный масштаб. Для вероятности ошибки используют логарифмический масштаб.
Из приведенных на рис. 12.6 данных вытекает, что наивысшая помехоустойчивость свойственна сигналам ФМ-2 и ФМ-4.
Контрольные вопросы
1. Запишите и поясните формулы вероятности ошибки двоичного символа сигналов ФМ-4, ФМ-8, КАМ-16. Сравните помехоустойчивость.
2. Объясните, почему с ростом числа позиций сигнала ухудшается помехоустойчивость.
Дата добавления: 2014-11-13; просмотров: 367; Мы поможем в написании вашей работы!; Нарушение авторских прав |