
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вероятность ошибки при оптимальной демодуляции одномерных сигналов цифровой модуляции
Как отмечалось в разд. 2, критерием оптимальности демодулятора является минимум полной вероятности ошибки решения относительно канального символа Рош. Но для пользователей количественной мерой помехоустойчивости цифровой системы передачи является вероятность ошибки бита р. В двоичных системах передачи вероятности Рош и р совпадают. В случае многоуровневых видов модуляции сначала находят Рош, затем рассчитывают р, зная модуляционный код.
В.А. Котельников ввел термин «потенциальная помехоустойчивость приема» – это максимальная помехоустойчивость, которую обеспечивает оптимальный демодулятор. В сущности, это помехоустойчивость используемого модулированного сигнала при заданных характеристиках канала связи.
Анализ вероятности ошибки начнем из рассмотрения одномерных двоичных сигналов. Воспользуемся результатами, полученными в разд. 2. На рис. 2.1, б для одномерного двоичного сигнала показаны сигнальное созвездие и условные плотности вероятности оценки  . Было сформулировано правило вынесения решения по результатам сравнения оценки
. Было сформулировано правило вынесения решения по результатам сравнения оценки  с граничным значением l: если
с граничным значением l: если  > l, то передавался символ s1(t), а если
> l, то передавался символ s1(t), а если  < l, то передавался символ s0(t). Оптимальное значение l находится посредине между а1 и а0:
< l, то передавался символ s0(t). Оптимальное значение l находится посредине между а1 и а0:
l = 0,5(а1 + а0). (11.1)
При этом вероятности ошибок при передаче сигналов s0(t) и s1(t) одинаковы и определяются выражением
 . (11.2)
. (11.2)
Условная плотность вероятности  имеет нормальное распределение вероятностей со средним значением равным a0. С учетом этого (11.2) запишется
имеет нормальное распределение вероятностей со средним значением равным a0. С учетом этого (11.2) запишется
 , (11.3)
, (11.3)
где sz – СКО шума на выходе согласованного фильтра, определенное раньше соотношением (5.14).
Примем в рассмотрение расстояние между сигналами
d = (а1 – а0). (11.4)
Из соотношений (11.1) и (11.4) получим
l = а0 + 0,5d (11.5)
С учетом (5.14) и (11.5) соотношение (11.3) дает вероятность ошибки канального символа в двоичной системе передачи
 . (11.6)
. (11.6)
Из определения гауссовой Q-функции  вытекает, что, чем большее значение аргумента, тем меньшее значение функции Q(z). Вероятность ошибки канального символа (11.6) будет уменьшаться при увеличении расстояния между сигналами d и уменьшении удельной мощности шума N0 на входе демодулятора.
вытекает, что, чем большее значение аргумента, тем меньшее значение функции Q(z). Вероятность ошибки канального символа (11.6) будет уменьшаться при увеличении расстояния между сигналами d и уменьшении удельной мощности шума N0 на входе демодулятора.
Дальше задача заключается в том, чтобы выразить расстояние между сигналами в (11.6) через физические параметры сигнала, действующего на входе демодулятора. Такими параметрами являются: средняя мощность модулированного сигнала Ps и скорость цифрового сигнала R или обратная к ней величина – длительность двоичного символа Тб = 1/R.
 Упражнение 11.1. Найдем вероятность ошибки для одномерных двоичных сигналов ФМ-2 и АИМ-2. На рис. 11.1 приведены сигнальные созвездия сигналов ФМ-2 и АИМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Еб = а2. Отсюда d = 2а = 2
Упражнение 11.1. Найдем вероятность ошибки для одномерных двоичных сигналов ФМ-2 и АИМ-2. На рис. 11.1 приведены сигнальные созвездия сигналов ФМ-2 и АИМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Еб = а2. Отсюда d = 2а = 2  . Вероятность ошибки бита определяется
. Вероятность ошибки бита определяется
 , (11.7)
, (11.7)
где  – отношение сигнал/шум.
– отношение сигнал/шум.
 Упражнение 11.2. Найдем вероятность ошибки для двоичного сигнала АМ-2. На рис. 11.2 приведено сигнальное созвездие сигнала АМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Е1 = а2, а Е0 = 0. Еб = 0,5(Е1 + Е0) = 0,5а2. Отсюда d = а =
Упражнение 11.2. Найдем вероятность ошибки для двоичного сигнала АМ-2. На рис. 11.2 приведено сигнальное созвездие сигнала АМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Е1 = а2, а Е0 = 0. Еб = 0,5(Е1 + Е0) = 0,5а2. Отсюда d = а = 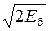 .
.
Вероятность ошибки бита определяется
 . (11.8)
. (11.8)
Перейдем к многопозиционным системам передачи, т.е. М > 2. Если канальные символы равновероятны, то вероятность ошибки канального символа определяется
 . (11.9)
. (11.9)
где Pош(si, sj) – вероятность ошибки в двоичной системе, использующей сигналы si и sj, а ошибка состоит в вынесении решения о передаче 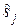 , если было передано si. Чтобы упростить расчеты, учитывают переходы лишь в ближайшие сигналы (это допустимо при высоких отношениях сигнал/шум, которые соответствуют вероятности ошибки Рош < 10–2). Переход от ошибки канального символа Рош к ошибке двоичного символа р выполняется легко, если используется модуляционный код Грея:
, если было передано si. Чтобы упростить расчеты, учитывают переходы лишь в ближайшие сигналы (это допустимо при высоких отношениях сигнал/шум, которые соответствуют вероятности ошибки Рош < 10–2). Переход от ошибки канального символа Рош к ошибке двоичного символа р выполняется легко, если используется модуляционный код Грея:
 . (11.10)
. (11.10)
 Упражнение 11.3. Найдем вероятность ошибки для многопозиционных одномерных сигналов АМ-М и АИМ-М. На рис. 11.3 приведены сигнальные созвездия сигналов АМ-4 и АИМ-4. Аналогично строятся созвездия при М > 4. Задачу будем решать для произвольного М (М – целая степень числа 2).
Упражнение 11.3. Найдем вероятность ошибки для многопозиционных одномерных сигналов АМ-М и АИМ-М. На рис. 11.3 приведены сигнальные созвездия сигналов АМ-4 и АИМ-4. Аналогично строятся созвездия при М > 4. Задачу будем решать для произвольного М (М – целая степень числа 2).
Коэффициенты аі принимают значение  . Определим среднюю энергию канального символа
. Определим среднюю энергию канального символа
 . (11.11)
. (11.11)
Учтем, что
d = 2a и  . (11.12)
. (11.12)
На основе (11.11) и (11.12) получим выражение для квадрата расстояния
 . (11.13)
. (11.13)
При анализе вероятности ошибки достаточно учесть переходы лишь в ближайшие канальные символы, поэтому
 . (11.14)
. (11.14)
Учитывая (11.10), (11.13) и (11.14) получим выражение вероятности ошибки двоичного символа
 . (11.15)
. (11.15)
Контрольные вопросы
1. Запишите и объясните формулу вероятности ошибки канального символа в двоичной системе передачи.
2. Объясните, что представляет собой величина 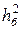 .
.
3. Объясните, какие упрощения допускают при анализе помехоустойчивости многопозиционных сигналов.
Дата добавления: 2014-11-13; просмотров: 422; Мы поможем в написании вашей работы!; Нарушение авторских прав |