Задача вычисления.

1. Интернет программалаулардың ерекше тенденциялар.
2. Интернет-экономика деген не?
3. Электронды бизнес деген не?
4. Корпоративтік web-сайт деген не?
5. Интернет магазин деген не?
6. Интернет аукцион деген не?
7. Ақпараттық бизнес портал деген не?
8. Интернет биржа деген не?
9. Интернет маркетинг деген не?
10. Интернет банкинг деген не?

Негізгі әдебиет: 13 нег [53-107], 14 нег [13-133]

Қосымша әдебиет: 1 қос [84-106 ], 3 қос [21-107 ]

ЛЕКЦИЯ №1

Задача вычисления.

Обычно задачу вычисления величины y по известной величине xзаписывают, с учетом интересующих нас причинно-следственных связей, в виде

(1)

Где yÎY, xÎX - элементы соответствующих функциональных пространств (как правило линейные, нормированные полные). A – оператор (правило), реализующий вычисления.

В первую очередь нас будут интересовать корректно поставленные задачи вычисления.

Задача вычисления называется корректно поставленной, если для любых входных данных из некоторого класса решение задачи существует, единственно и устойчиво по входным данным (т.е. непрерывно зависит от входных данных задачи).

При этом в первую очередь анализируют вопрос о вносимых в решение погрешностях

Есть четыре основных источника погрешности результата вычислений: математическая модель; исходные данные задачи; приближенный метод и погрешность при реализации вычислений (в частности погрешность округления):

- d₁y-погрешность математической модели, связана с физическими допущениями при выборе математической модели и на анализе этой погрешности мы останавливаться не будем;

- d₂y - погрешность исходных данных, порождает неустранимую погрешность решения

- d₃y - погрешность метода. Выражение A(x) , вообще говоря, не может быть просто численно реализовано. Задачу заменяют близкой задачей

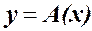(1')

мы переходим к другим функциональным пространствам , элементы которых допускают сравнительно простую численную реализацию. Соответствующим образом меняется и отображение .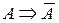

при этом естественно требовать, чтобы задача (1') была корректна, и чтобы решение `y было близко к решению y. величина

и представляет собой погрешность метода.

- d₄y - вычислительная погрешность. При численной реализации `y , которая по предположению возможна получают элемент , поскольку промежуточные результаты округлялись т.п. таким образом, вычислительная погрешность может быть записана в виде

полезно сразу же сформулировать некоторые эмпирические правила, которых придерживаются при реализации задачи вычисления:

1. при проведении вычислений нужно стремиться, чтобы погрешность метода d₃y была бы в несколько раз меньше неустранимой погрешности решения d₂y;

2. вычислительная погрешность d₄y должна быть существенно меньше всех остальных погрешностей решения, т.е. расчет нужно вести с таким количеством значащих цифр, чтобы погрешность округления была существенно меньше всех остальных погрешностей.

Рассмотрим пример, иллюстрирующий эти определения. Пусть необходимо вычислить интеграл , где F(x) задана таблично на [a, b]

Для получения приближенного решения можно поступить следующим образом: заменим на промежутке [a, b] функцию F(x) интерполяционным полиномом P_n(x) степени £ n, принимающим в точке x_i те же значения, что и F(x), (такой многочлен существует и единственен).

Вместо интеграла будем находить интеграл 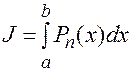, вычисление которого не составляет труда. В этом случае общая (полная) погрешность будет складываться из 3^-х частей:

1. Погрешностей, порождаемых неточностями исходных данных (т.е. табличными значениями Y=F(x)) – неустранимая погрешность;

2. Погрешности, порождаемой заменой F(x) полиномом P_n(x) – погрешность метода;

3. Погрешности округлений при вычислении -вычислительная погрешность.