
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Абсолютная и относительная погрешности
Остановимся несколько подробнее на анализе вычислительной погрешности d4y , возникающей из-за погрешностей округления при реализации численного алгоритма.
Если a – точное значение некоторой величины, а a* - известное приближение к нему (а @ a*), то погрешностью a* называют величину 
Абсолютной погрешностью a* называют некоторую величину  , про которую известно, что
, про которую известно, что
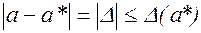 (1)
(1)
Относительной погрешностью называют некоторую величину  , про которую известно, что
, про которую известно, что
 (2)
(2)
Относительную погрешность часто выражают в %. Наименьшие из верхних границ в неравенствах, которые можно найти из имеющейся информации, называют предельной абсолютной и предельной относительной погрешностями соответственно.
Относительная ошибка определена, если знаменатель дроби не равен нулю, и нередко является полезной мерой достигнутой точности, поскольку меньше зависит от способа масштабирования данных. Так, если мы решим измерять веса в граммах, а не в килограммах, то относительная ошибка не изменится, тогда как ошибка умножится на 1000.
Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой.
Пример: а=0.04057 - 4 цифры, а=0.0405700 - 6 цифр. Абсолютную или относительную погрешность обычно записывают с 1 или 2 значащими цифрами
Информацию о том, что а* является приближенным значением числа а с абсолютной погрешностью  , иногда записывают в виде
, иногда записывают в виде  , числа а*,
, числа а*,  принято записывать с одинаковым числом значащих цифр после запятой а=1,123+-0,004 или а=1,123+-4 10-3. Это означает, что
принято записывать с одинаковым числом значащих цифр после запятой а=1,123+-0,004 или а=1,123+-4 10-3. Это означает, что
1,123-0,004<а<1,123+0,004.
Соответственно, а*, являющееся числом с относительной погрешностью  запишем в виде
запишем в виде 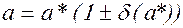
Дата добавления: 2014-12-03; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |