Схема единственного деления

Делим первое уравнение этой системы на коэффициент a₁₁ ¹ 0 при неизвестном х₁ (ведущий элемент).

Выполнения условия a₁₁¹ 0 можно добиться всегда путем перестановки уравнений системы.

(3) или

Исключаем неизвестное х₁ из остальных уравнений системы (для этого достаточно из каждого уравнения (i =2,3,…,n) вычесть уравнение (3), предварительно умноженное на коэффициент при х₁ , т.е. на a₂₁, a₃₁ и т.д. a_i1,

Например:

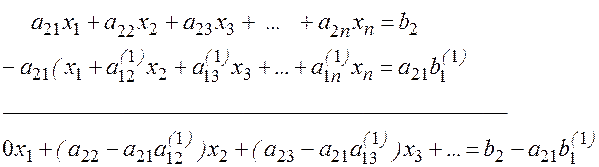
Обозначим

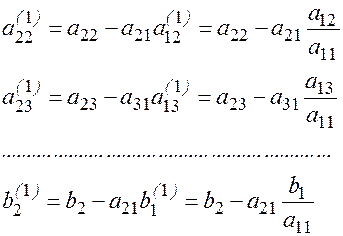
Преобразованные уравнения будут иметь вид:

. . . . . . . . . . . . . . . . .

Здесь обозначено

Матрица системы имеет вид:

Вслед за этим, оставив первое уравнение в покое, над остальными уравнениями системы совершим аналогичные преобразования:

1. выберем из их числа уравнение с ведущим элементом a₂₂⁽¹⁾

2. и исключим с его помощью из остальных уравнений неизвестное х₂.

3. Повторяя этот процесс n раз, вместо системы (2) получим равносильную ей систему с треугольной матрицей:

(4)

Матрицы такого вида называются верхними треугольными матрицами.

Из системы (4) последовательно находятся значения всех
неизвестных x_n, x_n-1, ..., x₁.

Таким образом, процесс решения (1) по методу Гаусса распадается на два этапа. Первый этап, состоящий в последовательном исключении неизвестных, называют прямым ходом. (число арифметических действий ¸ 2N³/3)

Обратным ходом. (число арифметических действий ¸ N²)

Общие формулы обратного хода имеют вид: