КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЛЕКЦИЯ № 4
Итерационные методы решения
систем линейных алгебраических уравнений.
При большом числе неизвестных линейной системы схема метода Гаусса, дающая точное решение, становится сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться приближенными численными методами. Привлекательным в итерационных методах является их самоисправляемость и простота реализации на ЭВМ.
Пусть дана система СЛАУ
Ах = b (1)
с неособенной матрицей А.
здесь 
-квадратная матрица размераn´n,
, 
-векторыn-гопорядка.
Чтобы применить к (1) метод итерации, необходимо привести (1) к виду:
х = aх + b (2)
здесь 
-квадратная матрица размераn´n,
, 
-векторы n-гопорядка.
СПОСОБ ПРИВЕДЕНИЯ СЛАУ ВИДА (1) к ВИДУ (2):
Предполагая, что диагональные элементы
,
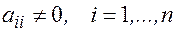разрешаем (1) относительно х.
Разделим i-ое уравнение системы Ах = b на диагональные элементы
В получившемся уравнении оставим в левой части уравнения хi , все остальное перенесем в правую часть уравнения:
обозначим 
,
Получаем систему уравнений, эквивалентную исходной системе, которая в матричной форме запишется в виде
х = aх + b,
причем: если в исходной матрице имелось диагональное преобладание, т.е.
то будем иметь 
< 1.
или
< 1.
Если в матрице А нет диагонального преобладания, его можно добиться каким-либо способом.
Систему (2) будем решать методом последовательных приближений.
Итерационный метод для начала вычисления требует задания одного или нескольких начальных приближений.
Строим последовательно столбцы:
- первое приближение
- второе приближение
Вообще говоря 
, k=0,1,2,… (3)
Последовательность приближений x(0) , x(1) ,…,x(k)
(k = 0,1,2, . . .) к решению х* системы (1) можно строить по рекуррентным формулам
.. (4),
при этом начальное приближение х(0) можно брать, вообще говоря, любое.
Итерационный процесс (4), начинающийся с некоторого вектора 
, будем называть методом простых итераций. (МПИ).
Запишем (4) в развернутом виде:
(5)
Если последовательность x(k) сходится, т. е. существует 
, то х* есть решение исходной системы (1).
В этом легко убедиться, если в (4) перейти к пределу при к®¥.
,
т. е. х* = aх* + b
Условия и скорость сходимости каждого итерационного процесса существенно зависят от свойств матрицы системы и выбора начальных приближений.
Теорема (достаточное условие сходимости МПИ):
Пусть 
. Тогда при любом начальном векторе 
метод простых итераций сходится к единственному решению 
задачи (1) и при всех 
справедливы оценки погрешности:
1. 
(6)
2. 
(7)
Доказательство:…………………………………………………………………………………..
Для того, чтобы метод простой итерации (4) сходился при любом х(0), необходимо и достаточно, чтобы |l(a)|<1, где l(a) - все собственные значения матрицы a.
При этом, если выполнено достаточное условие сходимости(||a||<1) , то необходимое и достаточное условие автоматически выполняется, ибо |l(a)|<||a||.
Чаще всего останавливаются на проверке двух условий:
1) 
2) 
Если одно из них выполняется, то метод итераций сходится при любом начальном приближении х(0).
Если требуется вычислить приближенное значение решения системы (1) с некоторой заданной степенью точности e т.е.
или
,
то из (6) можно получить условие окончания итерационного процесса
£ e
Тогда
или
Дата добавления: 2014-12-03; просмотров: 191; Мы поможем в написании вашей работы!; Нарушение авторских прав |