Метод итераций для системы двух уравнений.

Пусть даны два уравнения с двумя неизвестными

(1)

Действительные корни которых надо найти с заданной точностью.

Допускаем, что система (1) имеет лишь изолированные корни, число корней и их грубо приближенные значения можно установить, простроив кривые F₁(x, y) и F₂(x, y) определив координаты их точек пересечения.

Пусть x=x₀ и y=y₀- приближенные значения корней системы (1), полученные графическим способом или другим способом (грубой прикидкой).

Представим систему (1) в виде

(2)

И построим последовательные приближения по следующим формулам:

(3)

Если итерационный процесс (3) сходится, т. е. существуют пределы,

то, предполагая функции j₁(x, y) и j₂(x, y) непрерывными и переходя к пределу в (3), получим:

Отсюда

z = j₁(z , h); h = j₂(x , h),

Т.е. предельные значения z и h являются корнями системы (2), а следовательно, (1). Поэтому, взяв достаточно большое число итераций (3), получим x_n и y_n, которые будут отличаться от точных корней x=z и y=hсистемы (1) сколь угодно мало.

Теорема. Пусть в некоторой замкнутой окрестности
R {a £ x £ A; b £ y £ B} имеется одна пара корней x=z и y=h системы (2). Если:

1. Функции j₁(x, y) и j₂(x, y) определены и непрерывно дифференцируемы в R;

2. Начальные приближения x₀ , y₀ и все последующие
приближения x_n , y_n (n=1,2,…) принадлежат R;

3. В R выполнены равенства

то процесс последовательных приближений (3) сходится к корням x=z и y=h системы (2), т. е.

и

Замечание. Теорема остается верной, если условие 3) заменить на

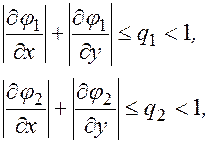или