КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Покажем единственность полинома Лагранжа.
Предположим обратное, пусть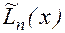 
- полином степени не выше n и
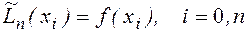
Тогда полином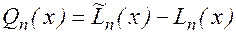 
- обращается в нуль в (n+1) точках x0 , x1 , ,xn и степени не выше n, т.е.
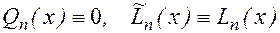
По следствию из основной теоремы алгебры многочленов – многочлен n –ой степени не может иметь более n корней.
Формуле Лагранжа можно придать более сжатый вид:
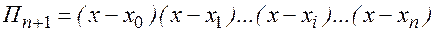
Дифференцируя по х это произведение, получим:
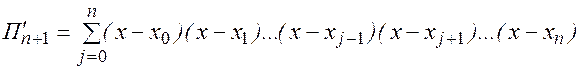При x=xi
Отсюда, получаем
Замечание. Нетрудно оценить число арифметических действий, в главном порядке по n это есть величина O(n2).
Рассмотрим 2 частных случая интерполяционного полинома Лагранжа.
При n =1 имеем 2 узла и формула Ln представляет собой уравнение прямой, проходящей через 2 заданные точки:
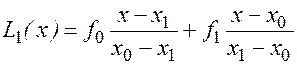
При n =2 получим уравнение параболы L2(x), проходящей через 3 точки:
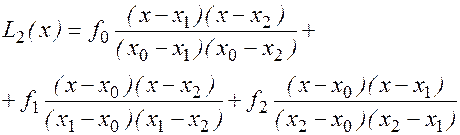
L1(x) и L2(x), называются соответственно формулами линейной и квадратичнойинтерполяции.
Дата добавления: 2014-12-03; просмотров: 193; Мы поможем в написании вашей работы!; Нарушение авторских прав |