КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка погрешности полиномиальной интерполяции.
Оценим остаточный член, т.е. разность Rn-(x)=f(x)-Ln(x)
Потребуем, чтобы в области [a, b] изменения x функция f(x) была дифференцируема (n+1) раз, т.е. f’(x),…, f(n+1) (x).
Ясно, что в узлах интерполяции эта погрешность Rn(x)=0.
Оценим ее в любой точке x Î [a, b].
Рассмотрим вспомогательную функцию
u(x)=f(x)-Ln(x)-kПn+1(x), где
- K - постоянный коэффициент, который выберем ниже.
U(x) имеет (n+1) нуль (корень) в т. x0, x1, …, xn.
Подберем k так, чтобы u(x) имела n+2 корень в любой фиксированной точке x’ отрезка [a, b], не совпадающий с узлами интерполирования. Т.е. u(x’)=0.
Положим f(x’)=Ln(x’)-kПn+1(x’).
Тогда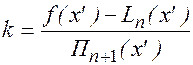 
При этом значении k функция u(x) будет иметь (n+2) корня в
узлах x’ ,x0, x1, …, xn.
Применяя теорему Ролля на каждом из отрезков [x0, x1],[x1, x2],…,
[xi, x’], [x’, xi],…,[xn-1, xn] убеждаемся, что производная u’(x) имеет не менее (n+1) корня на [a, b].
U’’(x) – n раз обращается в нуль на [a, b].
………………………………………………
U (n+1)(x) - имеет 1 корень
Пусть U (n+1)(x)=0, xÎ[a, b].
Так как Ln(n+1)(x)=0 и Пn+1(n+1)(x)=(n+1)!, имеем
При x=x, получаем
® 
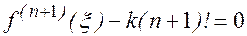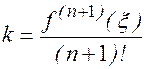
Т.о. Rn(x)=f(x)-Ln(x)=?
В силу того, что U(x’)=0, имеем
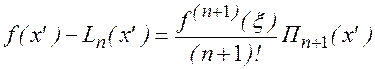
Т.к. x’ - произвольно, то
, где xÎ[a, b].
Обозначим через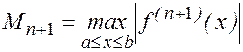 
Получим формулу для погрешности интерполяционной формулы Лагранжа
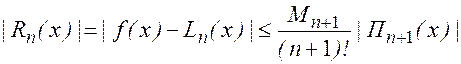
Если f(x) - многочлен n -ой степени, то f(x)=Ln(x) и Rn(x)=0 в силу единственности.
Пример:
С какой точностью можно вычислить Ö115 с помощью Ln(x) для y=Öx, если x0=100, x1=121, x2=144.
Y’=0.5x-1/2, y’’=-1/4x-3/2, y’’’=3/8x-5/2. M3=max|y’’|=3/8 1/Ö1005=3/2 10-5.
|R2|£3/8 10-5 1/3! |(115-100)(1150121)(115-144)|=1.6 10-3.
ЛЕКЦИЯ № 9
Интерполяционный многочлен Ньютона
с конечными разностями.
Зададимся целью придать интерполяционной формуле более простой вид, подобный широко используемой в математическом анализе формулы Тейлора.
Такая структура интерполяционного многочлена позволила бы более просто перестраивать его степень, добавляя или отбрасывая удаленные от начала его записи члены.
Будем считать, что интерполируемая функция y=f(x) задана своими значениями y0, y1,…, yn на системе равноотстоящих узлов
x0, x1, …, xn, т.е. таких, что любой узел этой сетки можно представит в виде
xi=x0+ih,
где i=0, 1,…,n, а h>0 - некоторая постоянная величина, называемая шагом сетки.
Прежде чем строить желаемые интерполяционные формулы, рассмотрим элементы конечных разностей.
Конечная разность 1- го порядка есть разность между значениями функции:
Конечная разность 2 – го порядка
Этот процесс построения разностей может быть продолжен, и описывается рекуррентной формулой, выражающей конечную разность
k - го порядка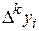 
через разности (k-1) порядка:
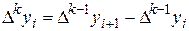
k=1, 2,…,, n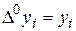 
Конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции (последние можно интерпретировать как конечные разности нулевого порядка). Эту общую таблицу называют таблицей конечных разностей.
| x0 | y0 | Dy0 | D2y0 | D3y0 | D4y0 | . |
| x1 | y1 | Dy1 | D2y1 | D3y1 | D4y1 | . |
| x2 | y2 | Dy2 | D2y2 | D3y2 | ||
| x3 | y3 | Dy3 | D2y3 | |||
| x4 | y4 | Dy4 | ||||
| x5 | y5 | |||||
| . | . |
Будем строить интерполяционный многочлен Pn(x) в форме:
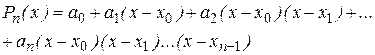(2)
Его n+1 коэффициент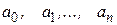 
будем находить последовательно из n+1 интерполяционных равенств
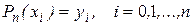,а именно, полагая i=0 , т.е. 
Имеем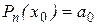 
, а по условию интерполяции 
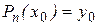, следовательно, 
Далее, при i=1 , аналогично получаем равенство
,
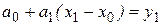в которое подставляем уже найденное значение .
Разрешая это равенство относительно, 
и используя обозначение конечной разности, получаем
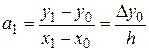
Следующий шаг, при i=2, дает
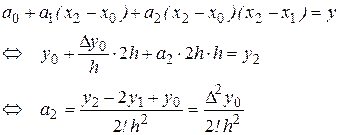
Полной индукцией можно доказать справедливость выражения
(3)
Подставляя найденные коэффициенты 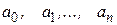в (2), получаем многочлен
,
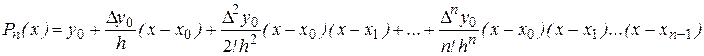(4)
который называют первым интерполяционным многочленом Ньютона..
Учитывая, что каждое слагаемое многочлена, начиная со второго, содержит множитель 
, естественно предположить, что этот многочлен наиболее приспособлен для интерполирования в окрестности узла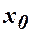 
( при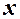 
, близких к , 
).
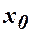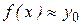Будем называть узел 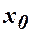базовым для многочлена (4), и упростим (4) введением новой переменной 
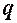равенством 
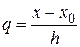, или (что - то же) равенством 
.
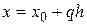Так как при любых
то в результате подстановки этих разностей в (4) приходим к первой интерполяционной формуле Ньютона в виде
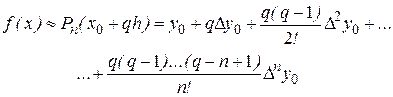(5)
где обозначение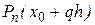 
указывает не только на n – ю степень многочлена, но и на базовый узел 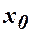и связь переменных 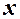и .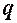
Первая формула Ньютона обычно применяется при значениях 
, а именно, для интерполирования вперед, ( при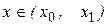 
,
т. е. при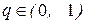 
) и экстраполирования назад (при 
,
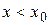т.е. при 
).
Для интерполирования в конце таблицы форма интерполяционного многочлена 
берется такой, которая предусматривает поочередное подключение узлов в обратном порядке: сначала последний, потом предпоследний и т. д., т. е.
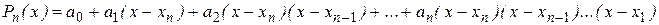(6)
Коэффициенты 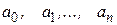этого многочлена находятся аналогично тому, как они находились для многочлена (2), только здесь подстановка узловых точек вместо 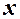и рассмотрение интерполяционных равенств производится тоже в обратном порядке.
Полагая 
, имеем:
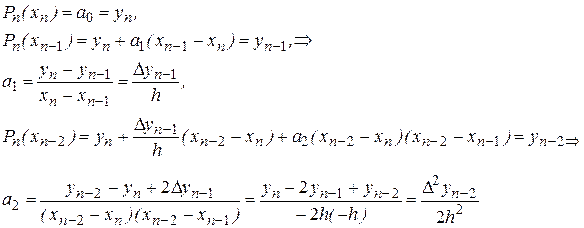
и т. д. В общем случае 
Таким образом, получаем второй интерполяционный многочлен Ньютона
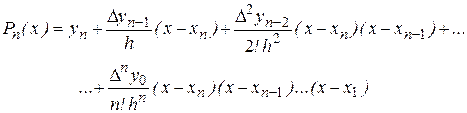(7)
В котором базовым является узел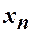 
и коэффициенты которого определяются конечными разностями, расположенными на восходящей диагонали от 
.
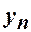Положим в (7)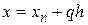 
, иначе, введем новую переменную 
и преобразуем к ней входящие в (7) разности:
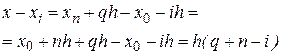
В результате приходим ко второй интерполяционной формуле Ньютона вида
(8)
Ее также целесообразно использовать при значениях , т.е. в окрестности узла 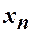для интерполирования назад (при 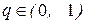) и эктраполирования вперед (при 
).
Наряду с выведенными специально для начала и конца таблицы первой и второй интерполяционными формулами Ньютона, имеется еще несколько формул, рассчитанных на их применение в центральной части таблицы (интерполяционная формула Стирлинга и формула Бесселя).
Теперь о том, как могут быть трансформированы остаточный член и его оценки при конечно – разностной интерполяции.
В силу доказанной единственности интерполяционного многочлена Лагранжа, все построенные здесь интерполяционные многочлены Ньютона – это всего лишь различные формы его представления. Следовательно, для всех этих форм справедливо выражение остаточного члена, полученного для многочлена Лагранжа.
где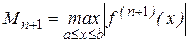 
Для случая равноотстоящих узлов 
многочлен 
преобразуется к новой переменной 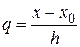следующим образом:
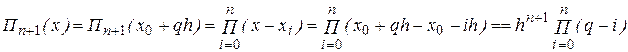
Отсюда
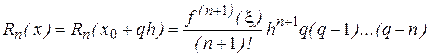
Итак, для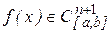 
,. конечно - разностная интерполяционная формула Ньютона степениn с базовым узлом 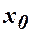может быть записана в виде
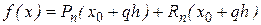, в котором 
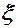- некоторая неизвестная, но фиксированная (при фиксированном 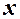) точка интервала 
.
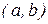Аналогично, при выборе базового узла 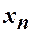, т. е. для второй интерполяционной формулы Ньютона, получаем точное представление
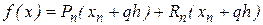, где
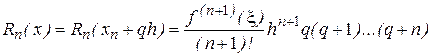
В силу связи (формула (1)) между производными и конечными разностями, выражение для (n+1) – ой производной
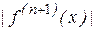
приближенно можно заменить на величину
.
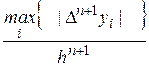В этом случае степень n интерполяционного многочлена должна быть заниженной по сравнению с n числом узлов (иначе конечная разность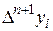 
(n+1) – го порядка равна нулю).
ЛЕКЦИЯ № 10
Метод наименьших квадратов и наилучшие среднеквадратические приближения.
Рассмотрим задачу, возникающую при изучении каких-либо закономерностей на основе наблюдения или экспериментов. Характерной особенностью таких задач является то, что исходный материал – заведомо приближенный, в силу неточности измерительных приборов, неповторимости условий наблюдений, случайных ошибок и пр.
Предположим, что между независимой переменной x и зависимой переменной y имеется некая неизвестная функциональная связь
y = f(x) .
Эта связь отображается таблицей
| x | x0 | x1 | … | xn |
| y | y0 | y1 | … | yn |
приближенных значений yi » f(xi) , получаемых в ходе наблюдений или экспериментов.
Требуется дать приближенное аналитическое описание этой связи, т.е. подобрать функцию j(x) такую, которая аппроксимировала бы на отрезке [x0 , xn] заданную отдельными приближенными значениями yi функцию f(x).
Для решения этой задачи заведомо неудачным является интерполяционный подход хотя бы потому, что функция j(x) такая, что
j(xi) = yi при всех iÎ {0,1,…,n} ,
будет мало похожа на искомую f(x), поскольку в ней отразятся все ошибки экспериментальных данных.
Это заставляет отказаться от идеи интерполяции и находить функцию j(x) такую, чтобы она хорошо отражала в среднем зависимость между x и y .
А именно, из каких-либо соображений (аналитических, графических или иных) аппроксимирующая функция j(x) берется из определенного m -параметрического семейства функций, и ее параметры подбираются так, чтобы сумма квадратов отклонений значений j(xi) от заданных приближенных значений yi была минимальной.
Такая функция (т.е. при таком оптимальном наборе параметров) будет наилучшей аппроксимацией f(x) среди функций выбранного семейства в смысле метода наименьших квадратов.
Ясно, что число данных приближенных значений yi в таблице должно быть не меньшим, чем число параметров в подбираемой зависимости j(x); как правило, считается, что n>>m .
Итак, согласно МНК, задаем семейство
Y=j(x, a1 , a2 ,…, am )
И ищем значения параметров a1 , a2 ,…, am (где m£ n), решая экстремальную задачу (задачу на экстремум функции)
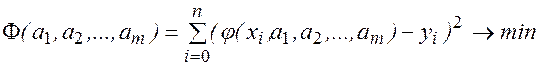
Оптимальный набор параметров , a*1 , a*2 ,…, a*m может быть найден из необходимых условий гладкого экстремума, т.е. в результате приравнивания к нулю частных производных функции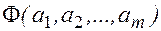 
, взятых по каждому из ее аргументов.
Получаем следующую систему уравнений относительно
неизвестных a1, a2,…,am
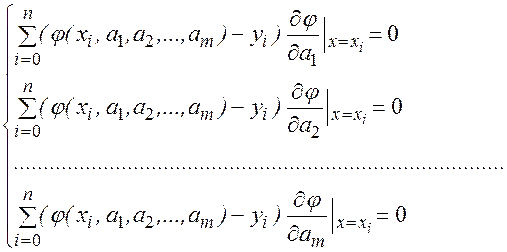(1)
Эти условия экстремума в силу специфики функции являются и достаточными условиями ее минимума.
В зависимости от характера табличных данных, (изучаемых с помощью графика), часто используют следующие
двухпараметрические семейства функций:
y=ax+b, y=a+blnx, y=ax b, y=1/(ax+b)
Трехпараметрические семейства: Y=ax2+bx+c, y=axb+c, y=aebx+c
При изучении периодических явлений применяют тригонометрические функции.
Рассмотрим, к чему сводится процесс построения наилучших среднеквадратических приближений в одном конкретном, но общем, случае, когда аппроксимирующая f(x) функция j(x) представляет собой линейную комбинацию нескольких других, вообще говоря, более простых (базисных) функций.
Пусть 
- некоторая заданная на [a, b] система линейно независимых функций.
Обобщенным многочленом будем называть функцию
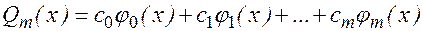(3)
Гдесi- произвольные вещественные числа (коэффициенты обобщенного многочлена).
Поскольку функции jj(x) считаются заданными, построение многочлена наилучшего приближения для данной функции f(x) сводится к нахождению оптимального набора c*0, c*1, ,c*m коэффициентов Qm(x) в (3) на основе метода наименьших квадратов, т.е. к решению задачи минимизации:
В дискретном случае необходимые и достаточные условия экстремума выражаются системой
(4)
После элементарных преобразований она может быть переписана в терминах скалярных произведений:
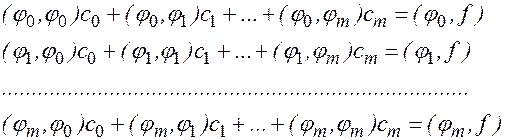(4)
Если сеточные функции jj(xi) образуют систему линейно независимых элементов пространства Rn+1[a, b], то полученная симметричная линейная алгебраическая система (4), называемая нормальной системой МНК, имеет заведомо отличный от нуля определитель, и значит, однозначно разрешима.
Следовательно, при заданном базисе путем решения системы (4) можно найти единственный обобщенный многочлен
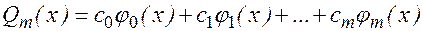
такой, что f(x) » Qm(x) при x Î[a, b} с наименьшей квадратичной ошибкой
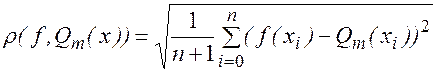
Дата добавления: 2014-12-03; просмотров: 204; Мы поможем в написании вашей работы!; Нарушение авторских прав |