Геометрический способ.

Пользуясь тем, что в точке известно и значение решения (согласно (2)), и значение его производной (согласно (1)), можно записать уравнение касательной к графику искомой функции 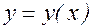в точке :

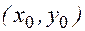(3)

При достаточно малом шаге h ордината

(3’)

этой касательной, полученная подстановкой в правую часть (3) значения , по непрерывности должна мало отличаться от ординаты решения задачи (1)-(2). Следовательно, точка пересечения касательной (3) с прямой 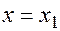может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую

,

которая уже приближенно отражает поведение касательной к 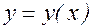в точке 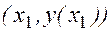. Подставляя сюда , иначе, пересекая эту «касательную» прямой , получим приближенные значения значением

и т. д. В итоге этого процесса, определяемого формулой

(4)

и называемого методом Эйлера, график решения 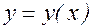данной задачи Коши (1)-(2) приближенно представляется ломаной, составленной из отрезков касательных (рис. 1), откуда происходит другое название метода – метод ломаных (4).

Рис. 1 Геометрическая интерпретация метода Эйлера.