
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение формулы Тейлора.
Линеаризуя решение в окрестности начальной точки по формуле Тейлора, имеем
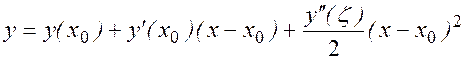
Отсюда при 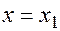 получаем
получаем
 (5)
(5)
Точное равенство (5), переписанное в виде
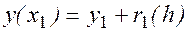
говорит о том, что здесь мы имеем одновременно как саму формулу Эйлера для вычисления значения 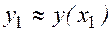 , так и ее остаточный член
, так и ее остаточный член
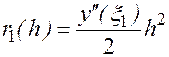 (6)
(6)
где x1 - некоторая точка интервала 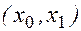 .
.
Остаточный член (6) характеризует локальную (или, иначе, шаговую) ошибку метода Эйлера, т. е. ошибку, совершаемую на одном шаге. Очевидно, что от шага к шагу, т. е. при многократном применении формулы (4), возможно наложение ошибок. За n шагов, т. е. в точке b, образуется глобальная ошибка; известный факт: порядок глобальной ошибки (относительно шага) на единицу ниже, чем порядок локальной ошибки, а порядком глобальной ошибки и определяется порядок соответствующего численного процесса задача Коши.
Таким образом, локальная ошибка метода Эйлера, согласно (6), есть O(h2) , глобальная - O(h), т.е. метод Эйлера относится к методам первого порядка.
- Квадратурный способ.
Начальную задачу для ОДУ (1)-(2) можно заменить эквивалентным интегральным уравнением.
 (7)
(7)
При 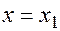 из него получится равенство
из него получится равенство
 (8)
(8)
Применение к интегралу в правой части равенства (8) простейшей одноточечной формулы прямоугольников дает приближенную формулу
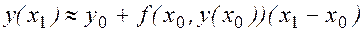
Правая часть которой, очевидно, совпадает с выражением (3) для подсчета значений  . В общем случае расчетная формула (4) метода Эйлера получается численным интегрированием посредством простейшей формулы левых прямоугольников в равенстве
. В общем случае расчетная формула (4) метода Эйлера получается численным интегрированием посредством простейшей формулы левых прямоугольников в равенстве
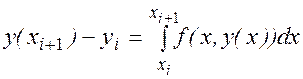 (9)
(9)
В предположении, что на каждом i - том шаге в роли начальной точки 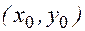 выступает точка
выступает точка 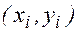 . зная точность используемой квадратурной формулы легко прийти к тому же выражению локальной ошибки метода Эйлера, что и при других способах его построения.
. зная точность используемой квадратурной формулы легко прийти к тому же выражению локальной ошибки метода Эйлера, что и при других способах его построения.
Несколько простых модификаций метода Эйлера.
Очевидно, применение к интегральному равенству (7) других простейших квадратурных формул будет порождать новые методы численного интегрирования задачи Коши (1)-(2).
Применение к интегралу в (9) простейшей квадратурной формулы трапеций приводит к неявному методу
 (11)
(11)
который будем называть методом трапеций. Квадратурная формула трапеций, как известно, на порядок точнее формул правых и левых прямоугольников. Отсюда вытекает более высокий (на единицу) порядок точности метода трапеций (11) по сравнению с явным и неявным методами Эйлера(4) и (10), т.е. метод трапеций (15) – это метод второго порядка.
Некоторый интерес представляет собой совместное применение явного метода Эйлера и неявного метода трапеций.
По форме (11) представляет собой скалярную задачу о неподвижной точке относительно неизвестного 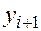 . поэтому, если в правую часть (15) подставить хорошее начальное приближение
. поэтому, если в правую часть (15) подставить хорошее начальное приближение 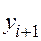 , подсчитываемое по формуле (4), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения. Таким образом, получаем гибридный (двухшаговый) метод
, подсчитываемое по формуле (4), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения. Таким образом, получаем гибридный (двухшаговый) метод
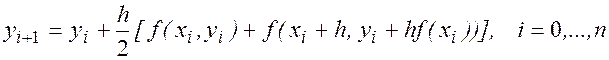
(12)
который называют методом Хойна (методом Эйлера-Коши) или методом с пересчетом.
Построим другую пару формул с погрешностью на шаге такого же порядка. Интеграл в правой части заменим по формуле средних прямоугольников:
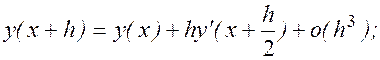 или
или
 ;
;
Если положить 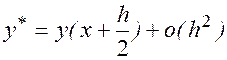 , то
, то  .
.
В качестве 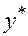 - грубого приближения можно взять результат по формуле Эйлера с шагом
- грубого приближения можно взять результат по формуле Эйлера с шагом 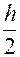 :
: 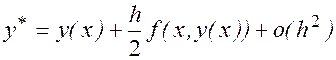
Этим соотношениям соответствуют расчетные формулы:
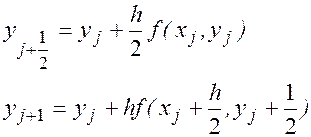 (14)
(14)
этот метод будем называть методом Эйлера на полуцелой сетке.
Полученные методы относятся к семейству методов Рунге-Кутта.
Методы Рунге – Кутта.
В процессе вычислений фиксированы некоторые числа:
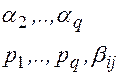 0<j<i
0<j<i  q;
q;
Последовательно получаем:
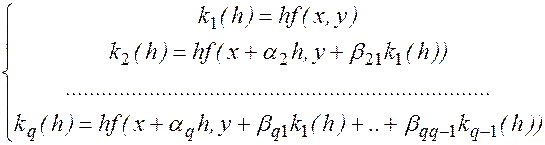
и полагаем 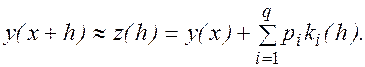
Рассмотрим вопрос о выборе параметров 
Обозначим 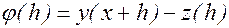 - погрешность на шаге.
- погрешность на шаге.
Если f(x,y)-гладкая функция своих аргументов, то 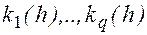 тоже гладкие функции параметра h.
тоже гладкие функции параметра h.
Пусть существуют производные  а
а  выбраны так что
выбраны так что 
Кроме того, предположим, что существует  , для которой
, для которой 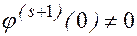 .
.
Согласно формуле Тейлора выполняется равенство:
 ,
,
где 0<  <1 (15)
<1 (15)
Величина  (h)-называется погрешностью метода на шаге, а s-порядок погрешности метода.
(h)-называется погрешностью метода на шаге, а s-порядок погрешности метода.
1. При q=1 имеем:

Равенство  выполняется для всех гладких функций f(x,y) только при
выполняется для всех гладких функций f(x,y) только при 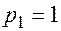 .
.
Этому значению 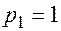 соответствует метод Эйлера. Для погрешности этого метода на шаге, согласно (15) получаем выражение:
соответствует метод Эйлера. Для погрешности этого метода на шаге, согласно (15) получаем выражение: 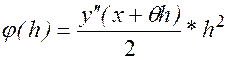 .
.
Таким образом, s=1. Это метод первого порядка точности.
2. Рассмотрим q=2:
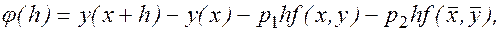 где
где 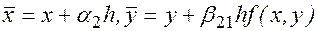 .
.
Вычисляем производные 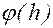 , находим:
, находим:
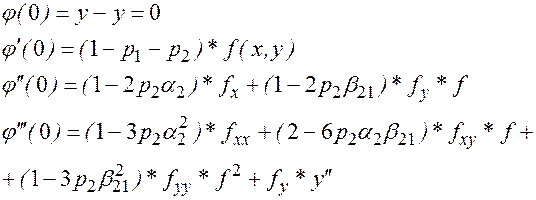
Соотношение  , если
, если 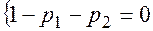
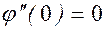 , если
, если 
Таким образом, 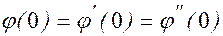 при всех
при всех 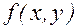 , если
, если

3 уравнения, 4 параметра. Задавая один из них произвольно, получим различные методы Рунге-Кутта с погрешностью второго порядка малости по h.
Например:
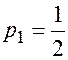
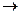
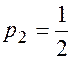 ,
, 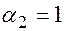 ,
, 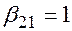 , что соответствует формулам (12) - метод Эйлера пересчётом.
, что соответствует формулам (12) - метод Эйлера пересчётом.
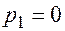
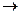
 ,
, 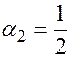 ,
,  , что соответствует формулам (14) - метод Эйлера с полуцелым шагом.
, что соответствует формулам (14) - метод Эйлера с полуцелым шагом.
Так как  , то нельзя построить формулы Рунге-Кутта с q=3, S=3;
, то нельзя построить формулы Рунге-Кутта с q=3, S=3;
3. Рассмотрим q=4, S=4.
 (16)
(16)
Один из точных методов, S=4, 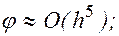 он носит название метода Рунге – Кутта.
он носит название метода Рунге – Кутта.
Численное решение дифференциальных уравнений высших порядков.
Рассмотрим однородное дифференциальное уравнение порядка (r)

Задача Коши: требуется найти частное решение, удовлетворяющее (r) начальным условиям:

Одним из способов численного решения начальных задач для дифференциальных уравнений высших порядков является их сведение к соответствующим задачам для систем уравнений первого порядка.
Заменой переменных сводим задачу к системе (r) уравнений 1-го порядка.
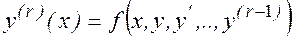
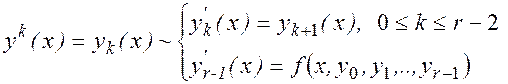
Например: 
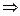
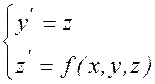 начальные условия перепишутся в виде
начальные условия перепишутся в виде 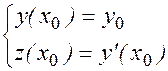 т. д.
т. д.
Методы Рунге-Кутта легко распространяются на системы дифференциальных уравнений 1-го порядка.
Например: рассмотрим систему 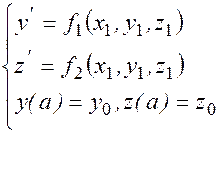
Приближённые решения 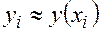 и
и 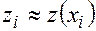 этой системы в точках
этой системы в точках 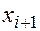 последовательно вычисляется по формулам:
последовательно вычисляется по формулам:
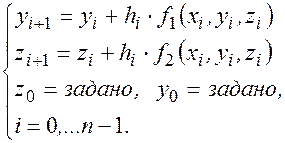 метод Эйлера
метод Эйлера
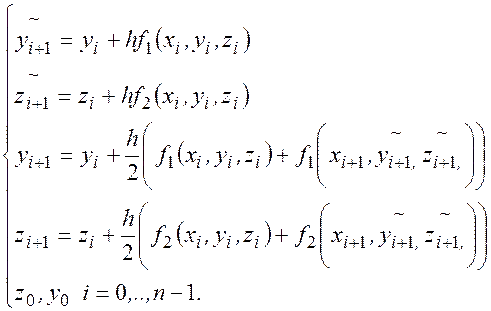
Метод Эйлера-Коши
Дата добавления: 2014-12-03; просмотров: 350; Мы поможем в написании вашей работы!; Нарушение авторских прав |