Разностные схемы для уравнений эллиптического типа.

Уравнение Лапласа является модельным для эллиптических уравнений в частных производных. Некоторые важные задачи, часто встречающиеся в приложениях, сводятся к решению одного эллиптического уравнения. К ним относятся задачи расчета дозвукового безвихревого (потенциального) течения газа и определения стационарного поля температуры в твердом теле, задачи гидродинамики и теплообмена.

Задача Дирихле (граничные условия первого рода) для уравнения Лапласа в прямоугольной области: найти непрерывную функцию U(x, y), удовлетворяющую внутри прямоугольной области
D{(x,y), }, уравнению Лапласа:

и принимающую на границе области заданные значения:

U(0,y)=f₁(y), U(a, y)=f₂(y), yÎ[0,b]

U(x,0)=f₃(x), U(x, b)=f₄(x), xÎ[0,a],

где f_i - заданные функции.

Будем считать, что U(x, y) непрерывной на границе области, т.е.

f₁(0)=f₃(0), f₁(b)=f₄(0),

f₂(0)=f₃(a), f₂(b)=f₄(a).

Выбрав шаги h и k - по x и по y соответственно, строим сетку

x_i=ih, i= 0, 1, ..., n; y_i=jk, j= 0, 1, ..., m; x_n=nh=a; y_m=mk=b.

Обозначим U_i,j = U(x_i , y_j), аппроксимируем частные производные

и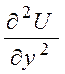

в каждом внутреннем узле сетки центральными производными второго порядка

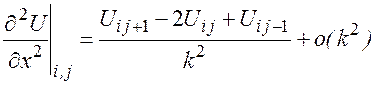
Заменим уравнение Лапласа его конечно - разностным аналогом