КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Разностные схемы для уравнения гиперболического типа.
Одномерным волновым уравнением называется следующее гиперболическое уравнение в частных производных:
, (1) 0<x<a, 0<t<T (1)
Это уравнение описывает распространение звуковых волн в однородной среде со скоростью с.
Существует уравнение первого порядка, свойства решений которого близки к свойствам решения уравнения (1):
(2)
Это уравнение называют одномерным линейным уравнение переноса, описывающим распространение волны со скоростью С вдоль оси X .
Точное аналитическое решение уравнения (2) с начальными данными
U(x,0)=f(x),
имеет вид
Рассмотрим конечно-разностные схемы для решения одномерного линейного волнового уравнения первого порядка.
- Явные методы Эйлера.
Погрешность аппроксимации: O(t, h) и O(t, h2) соответственно.
Разностные схемы явные, так как в каждое разностное уравнение входит лишь одно неизвестное
Анализ устойчивости разностных схем с помощью спектрального признака приводит к тому, что они обе абсолютнонеустойчивы и, следовательно, для численного решения волнового уравнения непригодны.
- множитель перехода для схемы с центральной разностью.
- Метод использования разностей против потока.
Простую явную схему Эйлера можно сделать устойчивой, если при аппроксимации производной по пространственной переменной использовать не разности вперед, а разности назад в тех случаях, когда скорость волны сположительна.
Если скорость волны сотрицательна, то устойчивость схемы обеспечивается при использовании разностей вперед.
С>0 разность назад
С<0 разность вперед
При использовании разностей назад разностные уравнения принимают вид
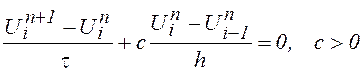
Эта разностная схема имеет первый порядок точности с погрешностью аппроксимации O(t, h).
Множитель перехода равен 
Из условия устойчивости следует, что схема устойчива при
то есть Сt/h £1
- Схема Лакса.
Разностную схему Эйлера можно сделать устойчивой, если заменить
на пространственное среднее 
В результате получим широко известную схему Лакса:
Это явная одношаговая схема с погрешность аппроксимации O(t, h2/t).
Множитель перехода равен 
Схема устойчива при 
– число Куранта
Отметим, что эта схема не всегда обладает условием согласованности, так как 
может не стремится к нулю при 
. Однако если число Куранта 
, то при 
условие согласованности выполняется.
Согласованной называется разностная схема, аппроксимирующая данное уравнение в частных производных, т. е. погрешность аппроксимации (разность между дифференциальным уравнением и его конечно-разностным аналогом) стремится к нулю при измельчении сетки.
- Неявный метод Эйлера
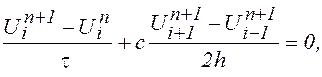
Погрешность аппроксимации 
Схема абсолютно устойчива, при использовании этой схемы приходится решать систему линейных алгебраических уравнений на каждом шаге по времени
Начальные условия заданы, матрица трех диагональная, применяем методпрогонки
При использовании неявных схем на каждом шаге по t приходится проводить больше вычислений, чем при использовании явных схем, но зато можно проводить расчеты с существенно большим шагом Dt.
- Метод с перешагиванием (чехарда)
Перейдем к схемам 2-го порядка точности.
Это трехслойная схема по времени, погрешность аппроксимации равна
. Метод устойчив при 
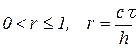
Недостатки:
· начальные условия нужно задавать на двух слоях по t ;
· связан с перешагиванием, т.е. 
не зависит от , что приводит к появлению двух независимых решений;
· высокие требования к памяти.
- Метод Лакса-Вендроффа
Схему Лакса-Вендроффа можно построить исходя из разложения в ряд Тейлора:
Из волнового уравнения следует
Заменив 
и 
на центральные разности 2-го порядка, получим:
Явная одношаговая схема 2-го порядка с погрешностью аппроксимации , устойчивая при
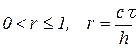
Множитель перехода:
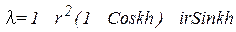
- Метод Мак-Кормака
Широко применяется для решения уравнений газовой динамики (нелинейных уравнения в частных производных).
Предиктор:
Корректор:
Отметим, что в предикторе – разность вперед, в корректоре – разность назад.
Можно поступить и наоборот, что бывает полезно при решении некоторых задач, например, задачи с движущимися разрывами.
- Центрированная по времени неявная схема.
Для построения неявной разностной схемы 2-го порядка вычтем 2 ряда Тейлора:
и заменим 
на 
В результате получим
Такое выражение для разностной производной называется конечно-разностной аппроксимацией по Кранку – Николсону.
Для линейного волнового уравнения имеем:
Подставляя вместо членов с производной по x - 
замену центральной разностью, получаем
Это схема имеет погрешность порядка , абсолютно устойчива, решается методом прогонки. Множитель перехода равен
При использовании методов повышенного порядка точности (3-го, 4-го) за увеличение точности приходится платить увеличением времени счета и усложнением разностной схемы. Это необходимо учитывать при выборе разностной схемы.
Обычно, для большинства приложений достаточную точность позволяют получить методы 2-го порядка точности.
При решении одномерного волнового (линейного) уравнения явные методы предпочтительнее, чем неявные, так как решение нестационарное (нас интересуют значения величин через небольшие промежутки времени)
Дата добавления: 2014-12-03; просмотров: 590; Мы поможем в написании вашей работы!; Нарушение авторских прав |