
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЛЕКЦИЯ № 14
Основные понятия теории разностных схем
Пусть на некотором отрезке D поставлена некоторая дифференциальная краевая задача.
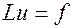 , (1)
, (1)
L - заданный дифференциальный оператор, f - заданная правая часть.
Будем предполагать, что решение u задачи (1) на отрезке 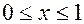 существует.
существует.
На отрезке D конечное число точек,  ,
,
Заменяем u(x) à таблицей 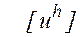 значений этого решения в
значений этого решения в
точках сетки  .
.
Предполагается, что сетка  зависит от параметра h>0.
зависит от параметра h>0.
Например, можно положить h=1/N , где N - некоторое натуральное число, и принять за сетку  совокупность точек
совокупность точек 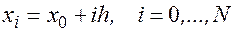 .
.
Искомая сеточная функция 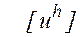 в этом случае в точке сетки
в этом случае в точке сетки 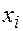 принимает значения
принимает значения 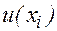 , которое будем обозначать
, которое будем обозначать 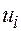 .
.
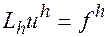 . (2)
. (2)
Назовем ее разностной краевой задачей (разностной схемой).
Определение 1.
Будем говорить, что решение 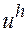 разностной краевой задачи (2) при сгущении сетки сходится к решению u дифференциальной краевой задачи (1), если
разностной краевой задачи (2) при сгущении сетки сходится к решению u дифференциальной краевой задачи (1), если
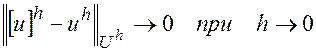 .
.
Если, сверх того, выполнено неравенство
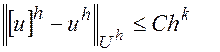 (3)
(3)
где С>0, k>o– некоторые постоянные, не зависящие от h, то будем говорить, что имеет место сходимость порядка hk или что разностная схема имеет k -й порядок точности.
В этом определении 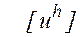 - проекция точного решения задачи (1) на сетку (
- проекция точного решения задачи (1) на сетку ( 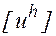 - сеточная функция, компоненты которой есть значения точного решения в
- сеточная функция, компоненты которой есть значения точного решения в
узлах сетки).
Предположим, что разностная задача (2) имеет единственное решение 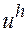 .
.
Если бы при подстановке в левую часть (2) вместо 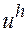 сеточной функции
сеточной функции 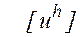 (проекции точного решения на сетку) равенство (2) оказалось бы в точности выполненным, то ввиду единственности решения имело бы место равенство
(проекции точного решения на сетку) равенство (2) оказалось бы в точности выполненным, то ввиду единственности решения имело бы место равенство 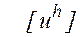 =
= 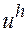 , идеальное с точки зрения сходимости.
, идеальное с точки зрения сходимости.
Это означало бы, что решение 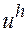 разностной задачи (2) совпадает с искомой сеточной функцией
разностной задачи (2) совпадает с искомой сеточной функцией 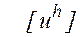 , которую мы условились считать точным решением.
, которую мы условились считать точным решением.
Однако, как правило, систему (2) не удается выбрать так, чтобы 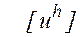 в точности ей удовлетворяла.
в точности ей удовлетворяла.
При подстановке в уравнение (2) возникает некоторая невязка:
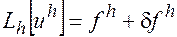
Если эта невязка 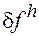 стремится к нулю при
стремится к нулю при 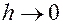 , так что
, так что 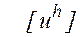 удовлетворяет уравнению (2) все точнее, то будем говорить:
удовлетворяет уравнению (2) все точнее, то будем говорить:
Определение 2.
Будем говорить, что разностная схема (2) аппроксимирует исходную дифференциальную задачу (1) на решении u, если
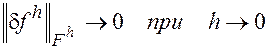
Если, сверх того, имеет место неравенство
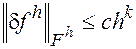 (4)
(4)
где С>0, k>o– некоторые постоянные, не зависящие от h, то будем говорить, что имеет место аппроксимация порядка hk или порядка к относительно величины h.
В случае аппроксимации можно считать, что уравнение (3) которому удовлетворяет 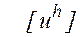 , получается из уравнения (2) путем прибавления к правой части некоторой малой (при малом h) добавки
, получается из уравнения (2) путем прибавления к правой части некоторой малой (при малом h) добавки 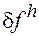 .
.
Следовательно, если решение 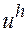 задачи (2) устойчиво относительно возмущения правой
задачи (2) устойчиво относительно возмущения правой 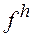 , т.е. мало изменяется при малом изменении правой части, то решение
, т.е. мало изменяется при малом изменении правой части, то решение 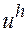 задачи (2) и решение
задачи (2) и решение 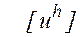 задачи (3) отличаются мало, так что из аппроксимации
задачи (3) отличаются мало, так что из аппроксимации
 при
при 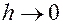 следует сходимость
следует сходимость
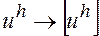 , при
, при 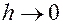
Определение 3.
Будем называть разностную схему (2) устойчивой, если существуют такие постоянные h0 и d0, что при любом h<h0 и любой сеточной функции eрÎFh, такой, что
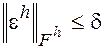 разностная задача
разностная задача
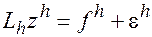 ,
,
полученная из (2) добавление к правой части возмущения eh имеет место и имеет только одно решение zh, причем справедлива оценка
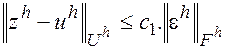 , (5)
, (5)
где С1 – некоторая постоянная, не зависящая от h.
Последнее неравенство означает, что малое возмущение eh правой части разностной схемы (2) вызывает равномерно относительно h малое возмущение (zh-uh)решения uh .
Определение 4.
Будем называть разностную схему (2) с линейным оператором Lhустойчивой, если при любой правой части fhÎFh уравнение 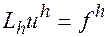 имеет единственное решение uhÎUh, причем
имеет единственное решение uhÎUh, причем
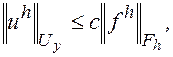 (6)
(6)
где С – некоторая постоянная, не зависящая от h.
Можно показать, в случае линейности разностного оператора Lh определения устойчивости 3 и 4 равносильны.
Теорема 1 (теорема Лакса о сходимости).
Пусть разностная схема (2) аппроксимирует задачу (1) на решении u с порядком hk и устойчива.
Тогда решение разностной задачи 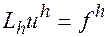 сходится к решению дифференциальной задачи
сходится к решению дифференциальной задачи 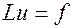 , причем имеет место оценка
, причем имеет место оценка
 ,
,
где С – некоторая постоянная, не зависящая от h.
Эта теорема позволяет свести вопрос о важнейшей с практической точки зрения проблеме исследования сходимостик вопросу исследования аппроксимации и устойчивости.
Доказательство:
Положим  и
и 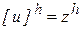 . Тогда определение устойчивости (5)
. Тогда определение устойчивости (5)
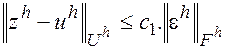 примет вид, (привлекая условие (4))
примет вид, (привлекая условие (4))
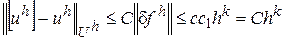
Дата добавления: 2014-12-03; просмотров: 306; Мы поможем в написании вашей работы!; Нарушение авторских прав |