Метод Ньютона для системы двух уравнений.

Пусть x_n, y_n - приближенные корни системы уравнений

F(x, y) = 0; (1)

G(x, y) = 0

Полагая x = x_n + h_n; y = y_n + k_n;

G(x_n + h_n; y_n + k_n) = 0

Отсюда, применяя формулу Тейлора и ограничиваясь линейными членами относительно h_n и k_n, будем иметь:

(3)

Если якобиан

То из системы (3) находим:

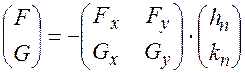
или

(4)

Следовательно, можно положить:

Исходные значения x₀ , y₀ определяются приближенно. Метод Ньютона будет сходиться квадратично, с другой стороны, каждая итерация требует решения системы линейных уравнений, а также метод Ньютона требует вычисления всех n² (n=2) первых частных производных нелинейных функций.

ЛЕКЦИЯ №9

Алгебраическая проблема собственных значений.

Вектор - собственный вектор матрицы A:

l - собственное значение матрицы A, или СЛАУ

Необходимо и достаточно:

(2)